Bewegungen und Kräfte sind eigentlich zwei eigenständige Themen. Aus der historischen Entwicklung heraus gehört die Betrachtung der Kräfte zu den Bewegungen, da sich wegen der Kräfte die Bewegungen verändern. Der gesamte Bereich kann dennoch unterteilt werden in die Kinematik, in der lediglich die Bewegungen untersucht werden, und die Dynamik, in der die Auswirkungen der Kräfte auf den Bewegungszustand untersucht werden.
Aristoteles unterteilte die Bewegungen in zwei Klassen: natürliche und erzwungene Bewegungen. Jede Bewegung, die einen Körper zu seinem ihm zustehenden Ort bringt, ist eine natürliche Bewegung und erfolgt von selbst. Demnach strebt Leichtes (Feuer und Luft) nach oben und Schweres (Wasser und Erde) nach unten. Die natürliche Bewegung erfolgt aus sich heraus, ist also eine Eigenschaft des Körpers.
Im Gegensatz dazu erfordert eine erzwungene Bewegung einen äußeren Beweger, der die Bewegung von ihrer natürlichen Richtung
ablenkt oder stoppt. Dieser äußere Beweger wird als ständig wirkende Kraft definiert, ohne die jede Bewegung irgendwann
aufhört. Aristoteles' Vorstellung bezüglich der Beschreibung von Bewegungen lassen sich so zusammenfassen:
Diese Erklärung von Bewegung wurde auch im europäischen Mittelalter noch genutzt. Bei der Erklärung der Wurfbewegung jedoch geriet man in Erklärungsnöte. Wenn jede Bewegung einen Beweger benötigte, warum bewegt sich ein einmal geworfener Stein so, wie man das beobachtete?
Zur Beantwortung dieser Frage sollte die sogenannte Impetus-Theorie führen, die im 13. und 14. Jahrhundert bedeutsam wurde. Aus
ihr entstammen fünf wesentliche Aussagen:
Der große Fortschritt der Impetustheorie bestand in dem Wegfall des äußeren Bewegers. Durch den Übergang der Kraft auf den sich
bewegenden Körper war es möglich, das Medium als Widerstand gegen eine Bewegung zu betrachten. Allerdings war die Kraft auch in
dieser Theorie immer noch die Ursache der Bewegung selbst.
In der Abbildung ist die Flugbahn einer Kanonenkugel nach der Impetus-Theorie zu sehen. Sie stand im Widerspruch zur Beobachtung, die so nicht erklärt werden konnte. Die Ursache für die gezeigte Flugbahn war die Eigenschaft des Impetus, verbraucht werden zu können. Ist der Impetus verbraucht, bewegt sich der Körper, hier die Kanonenkugel, in Richtung seines ihm zustehenden Ortes.
Wir müssen schließen, dass ein Beweger, wenn er einen Körper bewegt, diesem einen bestimmten Impetus aufdrückt, eine bestimmte Kraft, die diesen Körper in der Richtung weiterzubewegen vermag, die ihm der Beweger gegeben hat, sei es nach oben, nach unten, seitwärts oder im Kreis. Der mitgeteilte Impetus ist in dem gleichen Maße kraftvoller, je größer der Aufwand an Kraft ist, mit dem der Beweger dem Körper Geschwindigkeit verleiht. Durch diesen Impetus wird der Stein weiterbewegt, nachdem der Werfer aufgehört hat, ihn zu bewegen. Aber wegen des Widerstandes der Luft und auch der Schwerkraft des Steins, die ihn ständig in eine dem Streben des Impetus entgegengesetzte Richtung zwingen möchte, wird der Impetus immer schwächer. Darum muss die Bewegung des Steins allmählich immer langsamer werden. Schließlich ist der Impetus so weit geschwächt oder vernichtet, dass die Schwerkraft des Steins überwiegt und den Stein abwärts zu seinem natürlichen Ort bewegt.
Johannes Buridan (1295 - 1366)
Durch Galileo Galilei und insbesondere Isaac Newton (1643 - 1727) konnte der wesentliche Schritt zum heutigen Verständnis gemacht werden. Sie abstrahierten ihre Überlegungen von den tatsächlich beobachtbaren Phänomenen, indem sie nur das für die direkte Beschreibung notwendige beachteten. Dadurch kam es zu Ergebnissen, die nicht mehr unmittelbar verstanden werden konnten und die scheinbar im Widerspruch zu der Alltagswelt standen.
Aristoteles zeigt in einem Zitat die Problematik auf. Er lehnte die Existenz eines Vakuums, also eines vollständig leeren Raums, ab. Er argumentierte damit, dass jeder Körper im Vakuum absurde Bewegungen erfahren müsste. Da diese Bewegungen aber im Widerspruch zur Erfahrungswelt standen, konnte es notwendigerweise kein leeren Raum geben.
Niemand wäre in der Lage, einen Grund anzugeben, weshalb dasjenige, das in Bewegung gesetzt worden ist, irgendwo einmal stehen bleiben sollte. Denn wieso sollte dies eher hier als dort geschehen? Also wird (im Vakuum) alles entweder immer in Ruhe bleiben oder notwendigerweise ins Unbegrenzte weiterbewegt werden.
Aristoteles (384 - 322 v.Chr.)
Die Reduktion der Überlegungen auf das absolut Notwendige führte Galilei dann zu einer Vorstufe des Trägheitssatzes, indem er ideale, kaum irgendwo realisierbare Bedingungen annahm.
Wir müssen die Annahme machen, dass die Ebene sozusagen immateriell ist, oder zumindest sehr sorgfältig geglättet und absolut fest.. Und der in Bewegung befindliche Körper muss absolut glatt sein, von einer Gestalt, die der Bewegung keinen Widerstand entgegensetzt, z.B. von perfekter Kugelgestalt, und er muss aus dem härtesten Material bestehen oder sonst aus einer Flüssigkeit wie Wasser. Wenn alle diese Vorkehrungen getroffen sind, dann wird jeder Körper auf einer Ebene, die parallel zum Horizont verläuft, von der kleinsten Kraft bewegt werden, ja von einer Kraft, die geringer ist als jegliche gegebene Kraft.
Galileo Galilei (1564 - 1642)
Bis Galilei war die Kraft eine Eigenschaft eines Körpers, die die Bewegung des Körpers in der Form des Impetus ermöglichte. Die Kraft wurde auf den Körper übertragen. Seit Newton ist die Kraft ein Konzept, dass die Wechselwirkung eines Körpers mit einem zweiten Körper beschreibt. Damit wird auch klar, dass ein Körper alleine keine Kraft ausüben oder erfahren kann. Für die Ausübung einer Kraft ist ein zweiter Wechselwirkungspartner notwendig. Veränderungen des Bewegungszustands erfolgen nur, wenn ein zweiter Körper auf den bewegten Körper einwirkt, Verformungen erfolgen nur, wenn der Körper mit einem zweiten Körper wechselwirkt.
Bei der Wechselwirkung wird damit keine Kraft von einem zum anderen Körper übertragen, vielmehr wird die Kraft als Wechselwirkung zwischen zwei Körpern bezeichnet.
Seit Newton weiß man, dass der Naturzustand eines Körpers die gleichförmige Bewegung ist. Das ist die wesentliche Aussage aus dem
ersten Newtonschen Axiom:
Lex prima (Trägheitsgesetz)
Ein Körper verharrt im Zustand der Ruhe oder der gleichförmigen Translation, sofern er nicht durch einwirkende Kräfte zur Änderung seines Zustands gezwungen wird.
Der lateinische Originaltext:
Corpus omne perseverare in statu suo quiescendi vel movendi uniformiter in directum, nisi quatenus illud a viribus impressis cogitur statum suum mutare.
Eine direkte Folge des ersten Axioms ist das zweite Axiom, wonach die einwirkende Kraft proportional zur Änderung der Bewegung ist:
Lex secunda (Aktionsgesetz)
Die Änderung der Bewegung einer Masse ist der Einwirkung der bewegenden Kraft proportional und geschieht nach der Richtung derjenigen geraden Linie, nach welcher jene Kraft wirkt.
Der lateinische Originaltext:
Mutationem motus proportionalem esse vi motrici impressae, et fieri secundum lineam rectam qua vis illa imprimitur.
Kurz: $F = m \cdot a$
Lex tertia (Wechselwirkungsgesetz)
Kräfte treten immer paarweise auf. Übt ein Körper A auf einen anderen Körper B eine Kraft aus (actio), so wirkt eine gleich große, aber entgegen gerichtete Kraft von Körper B auf Körper A (reactio).
Der lateinische Originaltext:
Actioni contrariam semper et aequalem esse reactionem: sive corporum duorum actiones in se mutuo semper esse aequales et in partes contrarias dirigi.
Das dritte Axiom befasst sich damit, dass jede Kraft automatisch auch eine Gegenkraft bedingt. Die bekannte Formulierung actio = reactio ist insofern irreführend, da sie eine zunächst wirkende Kraft voraussetzt, auf die dann durch eine Gegenkraft reagiert wird. In Wirklichkeit wirken Kraft und Gegenkraft gleichzeitig.
Die Klassifizierung "actio" heißt vielmehr, dass diese Kraft die in der Anwendung interessierende Kraft darstellt, wohingegen die "reactio", also die Gegenkraft, im Grunde nicht interessiert bzw. sich auch nicht messbar auswirkt. Beispielsweise gibt es als "actio" die Gravitationskraft, d.h. ein Apfel wird von der Erde angezogen und in Richtung Erdmittelpunkt beschleunigt. Diese Kraft hat Auswirkungen, im wesentlichen auf den Apfel, der herunterfällt. Die "reactio" in diesem Beispiel wäre die anziehende Kraft des Apfels auf die Erde. Diese wird nämlich auch in Richtung des Apfelmittelpunkts beschleunigt, was sich aufgrund der großen Masse der Erde (2.Axiom) und deren Trägheit (1.Axiom) aber nicht bemerkbar macht.
Die Newtonschen Axiome sind die Grundpfeiler der Mechanik. Angefangen bei der gleichförmigen Bewegung als der natürliche Bewegungszustand eines Körpers, weitergehend mit der Notwendigkeit einer Kraft, um diesen Bewegungszustand zu ändern bis zu der zwingend notwendigen Gegenkraft, die gleichzeitig zu jeder wirkenden Kraft auftritt.
Als geradlinige Bewegungen werden diejenigen Bewegungen bezeichnet, deren Weg eine bestimmbare Länge besitzen, z.B. weil der Weg eine geometrische Figur beschreibt oder weil eine mathematische Funktion dahintersteht.
Die Bewegung der Erde um die Sonne ist eine Bewegung auf einer Kreisbahn. Diese Kreisbahn hat aber eine ganz bestimmte
Länge, in diesem Fall den Umfang eines Kreises mit dem Abstand der Erde von der Sonne als Radius, r = 150000000 km. Für den Umfang
gilt dann:
$$
U = 2 \cdot \pi \cdot r
$$
In diesem Beispiel wäre also die Länge des Weges, den die Erde im Laufe eines Jahres zurücklegt:
$$
U = 9,4 \cdot 10^8 \; \text{km}
$$
Der Begriff geradlinig ist also nicht wörtlich zu verstehen.
Der Weg, auf dem eine Bewegung stattfindet, wird i.A. mit dem Buchstaben $s$ bezeichnet. Die Standardeinheit für den Weg ist Meter. $$ \text{Strecke} \; s \\ [s] = 1 \; \text{m} $$ Für die Zeitspanne, die eine Bewegung andauert, wird der Buchstabe $t$ verwendet, mit der Einheit Sekunde. $$ \text{Zeit} \; t \\ [t] = 1 \; \text{s} $$
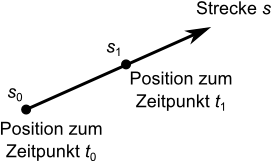Für die Beschreibung einer Bewegung ist es notwendig, die Veränderung der Position eines Objektes auf einer Strecke in
Abhängigkeit von der Zeit zu wissen.
Für die Veränderung der Position schreibt man $\Delta s$ und für die dafür benötigte Zeitspanne $\Delta t$. Der
Quotient aus den beiden Größen nennt man Geschwindigkeit $v$. Es gilt:
$$
v = \frac{\Delta s}{\Delta t} = \frac{s_1 - s_0}{t_1 - t_0}
$$
Die Größen $s_0$ und $t_0$ sind dabei immer die Größen am Anfang einer Messung. Die weiteren Größen, die im
Verlauf der Bewegung noch bestimmt werden, werden dann folgerichtig mit $s_1, t_1, s_2, t_2, $ usw. bezeichnet.
Im Gegensatz dazu bezeichnen die Größen $s$ und $t$ Variablen, d.h. unbekannte und veränderliche Größen.
Für die Geschwindigkeit $v$ erhält man die Einheit Meter pro Sekunde: $$ \text{Geschwindigkeit} \; v\\ [v]=1 \; \frac{\text{m}}{\text{s}}$$
Stellt man $v = \frac{\Delta s}{\Delta t}$ nach $\Delta s$ um, erhält man das Zeit-Weg-Gesetz: $$ \Delta s = v \cdot \Delta t $$
Die Strecke $s$ und die Zeit $t$ sind also proportional zueinander. Der Proportionalitätsfaktor ist dann die Geschwindigkeit $v$.
In manchen Fällen ist es sinnvoll, die zu beschreibende Bewegung als Diagramm darzustellen. Hier ist es üblich, auf der
$x-$Achse die Zeit $t$ aufzutragen und auf der $y-$Achse die Strecke $s$. Damit erhält man ein $t-s-$Diagramm:
Links ist der proportionale Verlauf der Strecke in Abhängigkeit von der Zeit zu sehen. Die Steigung der Geraden ist die
Geschwindigkeit, die somit auch mit Hilfe des Steigungsdreiecks ermittelt werden kann.
Rechts ist die Gerade um $s_0$ nach oben verschoben. Die Steigung und damit die Geschwindigkeit ist dieselbe wie in der linken
Abbildung.
Proportional bedeutet, dass die Gerade durch den Koordinatenursprung verlaufen muss. Daher ist in diesem Fall $s_0 = 0$ und $t_0 = 0$. So entsteht aus $ \Delta s = v \cdot \Delta t$: \begin{align} \left( s_1 - s_0 \right) & = v \cdot \left( t_1 - t_0 \right) \\ s_1 & = v \cdot t_1 \\ s(t) & = v \cdot t \end{align}
In der rechten Abbildung ist $s_0 \neq 0$, daher folgt aus $ \Delta s = v \cdot \Delta t$: \begin{align} \left( s_1 - s_0 \right) & = v \cdot \left( t_1 - t_0 \right) \\ s_1 & = v \cdot t_1 + s_0 \\ s(t) & = v \cdot t + s_0 \end{align}
Eine andere Form der Darstellung ist das $t-v-$Diagramm. Hier wird auf der $y-$Achse die Geschwindigkeit $v$ aufgetragen.
Das in der Abbildung markierte Viereck hat die Kantenlängen $a = v_1$ und $b = t_2 - t_1 = \Delta t$. Der Flächeninhalt des
Viereckes ist demnach $A = a \cdot b = v_1 \cdot \Delta t$. Das wiederum ist gleich der Strecke $s = v_1 \cdot \Delta t$.
In einem $t-v-$Diagramm kann man also die mit einer Geschwindigkeit $v$ zurückgelegten Strecke $s$ bestimmen, indem man
die Fläche unter der Geraden in dem betrachteten Zeitintervall $\Delta t$ berechnet.
Der Fall $s_0 \neq 0$ muss allerdings extra berücksichtigt werden, da der Fall im $t-v-$Diagramm nicht zu erkennen ist.
Im $t-v-$Diagramm wird deutlich, dass sich die Geschwindigkeit der Bewegung im Verlauf der Zeit nicht verändert. Man hat also eine konstante Geschwindigkeit. Ist das bei einer Bewegung der Fall, spricht man von einer gleichförmigen Bewegung.
In diesem Abschnitt sollen Ansätze für die Bearbeitung verschiedener Aufgaben aus dem Bereich der gleichförmigen Bewegungen gezeigt werden. Dabei soll bitte beachtet werden, dass es jeweils nur eine von mehreren Möglichkeiten ist, die entsprechende Aufgabe zu lösen. Andere Wege oder andere Ansätze sind auch (fast) immer möglich.
• Einfache Bewegung
Ein Radfahrer fährt mit einer konstanten Geschwindigkeit von A-dorf nach B-stedt. Beide Orte liegen 12 km voneinander entfernt. Der Radfahrer benötigt 45 Minuten für die Fahrt.
Berechne die durchschnittliche Geschwindigkeit des Radfahrers.
Es gilt:
\begin{align} v &= \frac{\Delta s}{\Delta t} \\ \\ v &= \frac{12 \text{ km}}{45 \text{ min}} \\ \\ v &= \frac{12 \text{ km}}{0,75 \text{ h}} \\ \\ v &= 16 \; \frac{\text{km}}{\text{h}} \end{align}Zu beachten ist hier auf jeden Fall, dass die Einheiten richtig eingesetzt werden. Eine Geschwindigkeitseinheit km/min ist zwar möglich und nicht falsch, aber unüblich. Die Einheit km/h ist üblich und für solche Bewegungsaufgaben, d.h. Aufgaben, in denen alltägliche Bewegungen beschrieben werden sollen, auch angemessen. Die eigentlich richtige Einheit ist allerdings m/s und würde in dem Beispiel noch eine Umrechnung erfordern $\left( v = 4,44 \; \frac{\text{m}}{\text{s}}\right)$
• Zwei Bewegungen in dieselbe Richtung
Ein 100 m-Läufer startet bei $t = 0 \text{ s}$ und läuft mit einer durchschnittlichen Geschwindigkeit von $v = 8 \; \frac{\text{m}}{\text{s}}$. Ein zweiter Läufer startet etwas später, nämlich bei $t = 2 \text { s}$ und läuft durchschnittlich mit $v = 10 \; \frac{\text{m}}{\text{s}}$.
Wer erreicht das Ziel zuerst?
Eine solche Aufgabe lässt sich oft mit dem $t - s-$Diagramm lösen.
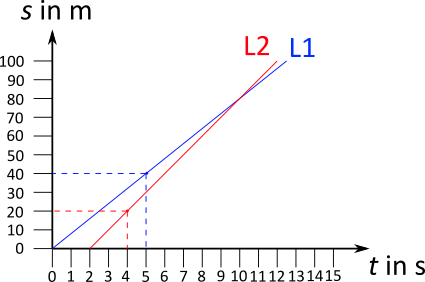
Zur Erstellung des Diagramms ist es sinnvoll, sich Punkte zu überlegen, die einfach in das Diagramm eingetragen werden können. Für den ersten Läufer ist das neben dem Punkt im Ursprung (Start bei t = 0 s) der Punkt bei 5 s und 40 m, denn 8 m/s bedeutet 16 m in 2 s und eben auch 40 m in 5 s. Bei dem zweiten Läufer kann man aus 10 m/s ganz einfach 100 m in 10 s machen. Zusammen mit dem um zwei Sekunden späteren Start ergibt das den Punkt 12 s und 100 m oder, wie im Diagramm markiert, 4 s und 20 m.
Die Frage, wer das Ziel zuerst erreicht, kann so sehr einfach beantwortet werden: Es ist Läufer Zwei.
Sollte die Frage jedoch lauten, wann und wo Läufer Zwei Läufer Eins überholt, d.h. wo sich der Schnittpunkt der beiden Geraden befindet, reicht das Diagramm u.U. nicht aus, da die Genauigkeit fehlt.
In einem solchen Fall bietet es sich an, mit dem Zeit-Weg-Gesetz zu arbeiten.
Es gilt:
\begin{align} s_1(t) &= 8 \; \frac{\text{m}}{\text{s}} \cdot t_1 \\ s_2 (t) &= 10 \; \frac{\text{m}}{\text{s}} \cdot t_2 \end{align}$s_1$ und $s_2$ sind gleich: $s_1 = s_2 = 100 \text{ m}$. Für die Zeit $t_2$ gilt: $t_1 - 2 \text{ s}$, da Läufer 2 zwei Sekunden später startet. Es folgen die beiden Gleichungen:
\begin{align} 100 \text{ m} &= 8 \; \frac{\text{m}}{\text{s}} \cdot t_1 \\ 100 \text{ m} &= 10 \; \frac{\text{m}}{\text{s}} \cdot \left(t_1 - 2 \text{ s} \right) \end{align}Gleichsetzen liefert:
\begin{align} 8 \; \frac{\text{m}}{\text{s}} \cdot t_1 &= 10 \; \frac{\text{m}}{\text{s}} \cdot \left(t_1 - 2 \text{ s} \right) \\ \\ 8 \; \frac{\text{m}}{\text{s}} \cdot t_1 &= 10 \; \frac{\text{m}}{\text{s}} \cdot t_1 - 20 \text{ m} \\ 8 \; \frac{\text{m}}{\text{s}} \cdot t_1 - 10 \; \frac{\text{m}}{\text{s}} \cdot t_1 &= - 20 \text{ m} \\ - 2 \; \frac{\text{m}}{\text{s}} \cdot t_1 &= - 20 \text{ m} \\ 2 \; \frac{\text{m}}{\text{s}} \cdot t_1 &= 20 \text{ m} \\ t_1 &= \frac{20 \text{ m}}{2 \; \frac{\text{m}}{\text{s}}} \\ t_1 &= 10 \text{ s} \end{align}Mit der Information kann nun auch der Ort angegeben werden:
\begin{align} s_1 (10 \text{ s}) &= 8 \; \frac{\text{m}}{\text{s}} \cdot 10 \text{ s} \\ s_1 &= 80 \text{ m} \end{align}Läufer 1 wird also nach 10 s und 80 m von Läufer 2 überholt.
• Zwei Bewegungen in entgegengesetzter Richtung
Ein Auto fährt von Braunschweig ins 335 km entfernte Frankfurt am Main. Gleichzeitig fährt in Frankfurt ein zweites Auto in Richtung Braunschweig los. Das erste Auto fährt mit durchschnittlich 75 km/h, das zweite mit durchschnittlich 60 km/h.
Wann und wo fahren sie aneinander vorbei?
Hier ist zunächst eine Skizze angebracht, um sich die Zeit-Weg-Gesetze beider Bewegungen klar zu machen.
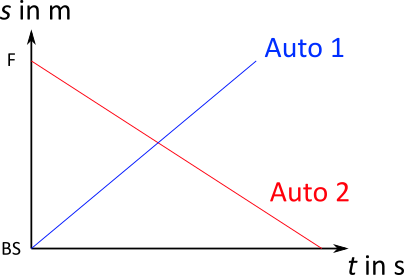
Der Ursprung des Koordinatensystems liegt in Braunschweig. Für Auto EIns folgt also, dass es sich mit einer positiven Geschwindigkeit bewegt. Für Auto Zwei widerum folgt, dass es sich mit einer negativen Geschwindigkeit bewegt. Weiterhin muss die Bewegungsgerade für Auto Zwei um 335 km nach oben verschoben werden. Es folgen:
\begin{align} s_1 (t) &= 75 \; \frac{\text{km}}{\text{h}} \cdot t_1 \\ \\ s_2 (t) &= - 60 \; \frac{\text{km}}{\text{h}} \cdot t_2 + 335 \text{ km} \end{align}Für den Punkt der Vorbeifahrt beider Autos gilt, dass die Zeiten $t_1$ und $t_2$ identisch sein müssen. Weiterhin wird nun gefordert, dass genau zu dem Zeitpunkt $t_1 = t_2 = t$ auch der Ort gleich sein muss $(s_1 = s_2)$. Damit folgt:
\begin{align} 75 \; \frac{\text{km}}{\text{h}} \cdot t &= - 60 \; \frac{\text{km}}{\text{h}} \cdot t + 335 \text{ km} \\ 135 \; \frac{\text{km}}{\text{h}} \cdot t &= 335 \text{ km} \\ t &= \frac{335 \text{ km}}{135 \; \frac{\text{km}}{\text{h}}} \\ t &= 2,481 \text{ h} \\ \\ s_1 (2,481 \text{ h}) &= 75 \; \frac{\text{km}}{\text{h}} \cdot 2,481 \text{ h} \\ s_1 &= 186,1 \text{ km} \end{align}Die Vorbeifahrt findet somit nach ca. 2,5 Stunden 186 km von Braunschweig entfernt statt (Das ist etwa auf halber Strecke zwischen Kassel und dem Hattenbacher Dreieck, dem Übergang von der A7 auf die A5).
Verändert sich die Geschwindigkeit, spricht man von einer ungleichförmigen Bewegung. Für diesen Fall betrachtet man die Veränderung der Geschwindigkeit, analog zur Veränderung der Position bei den gleichförmigen Bewegungen: $$ a = \frac{\Delta v}{\Delta t} = \frac{v_1 - v_0}{t_1 - t_0} $$ Dabei wird die Beschleunigung $a$ definiert als die Veränderung der Geschwindigkeit in einem Zeitintervall. Dabei erhält man als Einheit für die Beschleunigung Meter pro Sekunde zum Quadrat. $$ \text{Beschleunigung} \; a \\ [a] = 1 \; \frac{\text{m}}{\text{s}^2} $$
Ebenfall analog zu den oben genannten Fällen ergibt sich im $t-v-$Diagramm eine Gerade mit der Steigung $a$.
$$
\Delta v = a \cdot \Delta t
$$
$$
v_1 = a \cdot \Delta t + v_0
$$
Zusammen mit $t_0 = 0$ und $v_0 \neq 0$ ergibt sich:
$$
v(t)=a \cdot t+v_0
$$
Der zurückgelegte Weg $s$ wird ebenfalls berechnet, indem man die Fläche unter der Geraden berechnet:
$$
A = s = v_1 \cdot \Delta t + \frac{1}{2} \Delta v \cdot \Delta t
$$
Der Summand $v_1 \cdot \Delta t$ ist durch das lila Viereck gekennzeichnet, der Summand $\frac{1}{2} \Delta v \cdot \Delta t$
durch das blaue Dreieck.
Wird nun noch das $\Delta v$ durch den Ausdruck $a \cdot \Delta t$ ersetzt, erhält man:
$$
\Delta s = v_1 \cdot \Delta t + \frac{1}{2} a \cdot \Delta t^2 \\
s_1 = \frac{1}{2} a \cdot \Delta t^2 + v_1 \cdot \Delta t + s_0
$$
Gilt nun noch, dass $t_0 = 0$ und $s_0 \neq 0$ ist, folgt:
$$
s(t) = \frac{1}{2} a \cdot t^2 + v_0 \cdot t + s_0 \\
v(t)= a \cdot t + v_0
$$
Mit diesen beiden Gleichungen lassen sich eigentlich alle Bewegungsaufgaben lösen, denn auch die gleichförmige Bewegung ist in ihnen enthalten. Bei der gleichförmigen Bewegung ist die Geschwindigkeit konstant, d.h. die Geschwindigkeitsänderung und damit die Beschleunigung ist Null. Damit entfällt der Term $\frac{1}{2}a \cdot t^2$ bzw. der Term $a \cdot t$.
Die ungleichförmigen Bewegungen werden auch nochmal unterteilt in den bis eben beschriebenen Fall der gleichmäßig beschleunigten Bewegung mit einer konstanten Beschleunigung $a$ und den Fall der ungleichmäßig beschleunigten Bewegung, bei der auch die Beschleunigung zeitabhängig ist, also $a(t)$ gilt.
• Einfache beschleunigte Bewegung - 1
Ein Fahrzeug wird in fünf Sekunden von 0 auf 100 km/h beschleunigt.
Bestimme die Beschleunigung.
Es gilt der Zusammenhang
\begin{align} a &= \frac{\Delta v}{\Delta t} \\ \\ a &= \frac{v_1 - v_0}{t_1 - t_0} \\ \\ a &= \frac{100 - 0 \; \frac{\text{km}}{\text{h}}}{5 \text{ s}} \\ \\ a &= \frac{100 \; \frac{\text{km}}{\text{h}}}{5 \text{ s}} \end{align}Die Geschwindigkeit muss in $\frac{m}{s}$ umgerechnet werden:
\begin{align} 100 \; \frac{\text{km}}{\text{h}} &= 100 \; \frac{1000 \text{ m}}{3600 \text{ s}} \\ &= 27,78 \; \frac{\text{m}}{\text{s}} \end{align}Es folgt:
\begin{align} a &= \frac{27,78 \; \frac{\text{m}}{\text{s}} }{5 \text{ s}} \\ \\ a &= 5,56 \; \frac{\text{m}}{\text{s}^2} \end{align}• Einfache beschleunigte Bewegung - 2
Ein Fahrzeug beschleunigt mit $a = 2 \; \frac{\text{m}}{\text{s}^2}$ auf einer Strecke von $s = 1200 \text{ m}$ aus dem Stillstand.
Berechne die Geschwindigkeit des Fahrzeugs am Ende der Beschleunigung.
Es gelten die Zusammenhänge:
\begin{align} s &= \frac12 a t^2 \\ v &= at \end{align}$v = at$ wird nach der Zeit umgestellt $(t = \frac{v}{a})$ und in die andere Gleichung eingesetzt.
\begin{align} s &= \frac12 a \left( \frac{v}{a} \right)^2 \\ \\ s &= \frac{v^2}{2a} \end{align}Gesucht ist die Geschwindigkeit, nach der die Gleichung umgestellt werden muss.
\begin{align} v &= \sqrt{2as} \\ \\ v &= \sqrt{2 \cdot 2 \; \frac{\text{m}}{\text{s}^2} \cdot 1200 \text{ m}} \\ \\ v &= 69,28 \; \frac{\text{m}}{\text{s}} \\ v &= 249,41 \; \frac{\text{km}}{\text{h}} \end{align}In diesem Zusammenhang wurden zwei weitere Gleichungen, die bei beschleunigten Bewegungen eine Rolle spielen können, entwickelt (plus eine dritte, die entsprechend durch Umstellung entsteht).
$$ s = \frac{v^2}{2a} \\ \\ v = \sqrt{2as} \\ \\ a = \frac{v^2}{2s} $$Wenn die Zeit bei der Bearbeitung der Aufgabe keine Rolle spielt, und nur die Größen $s$, $v$ und $a$ vorkommen, können diese neuen Zusammenhänge genutzt werden.
• Gleichförmige und beschleunigte Bewegung nacheinander
Ein Auto rollt 30 Sekunden mit konstant 54 km/h eine Straße entlang. Dann wird das Auto innerhalb von 10 Sekunden auf 72 km/h beschleunigt und fährt so noch weitere 20 Sekunden.
Wie weit ist das Auto insgesamt gekommen?
Zunächst sollte eine Skizze eines $t-v-$Diagramms angefertigt werden, um sich über den Ablauf im Klaren zu sein. Die Geschwindigkeiten $v = 54 \; \frac{\text{km}}{\text{h}} = 15 \; \frac{\text{m}}{\text{s}}$ sowie $v = 72 \; \frac{\text{km}}{\text{h}} = 20 \; \frac{\text{m}}{\text{s}}$ sollten umgerechnet werden. Die Alternative wäre eine Umrechnung der Zeiten, z.B. $t = 30 \text{ s} = 0,0083 \text{ h}$. Das wäre aber nicht sinnvoll.
Bei der Erstellung des Diagramms ist es wichtig, das die Einheiten der Größen, die als $x-$ bzw. $y-$Achse dienen, zusammenpassen, also z.B. $\frac{m}{s}$ und $s$ (wobei die Strecke in $m$ herauskommt) oder $\frac{km}{h}$ und $h$ (mit der Strecke in $km$). Wenig sinnvoll, aber möglich ist auch $\frac{\text{Lichtjahr}}{\text{Woche}}$ und $\text{Woche}$ mit der Strecke in $\text{Lichtjahren}$.
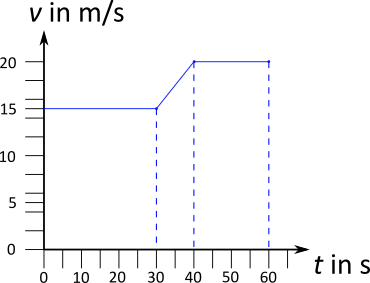
Aus der Fläche unter dem Graphen im $t-v-$Diagramm kann die zurückgelegte Strecke bestimmt werden. Dazu werden die unterschiedlichen Flächenstücke farbig markiert.
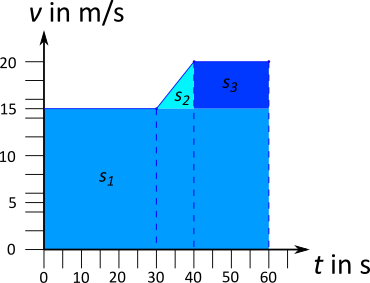
Für die einzelnen Flächen folgen die Flächeninhalte:
\begin{align} s_1 &= 15 \; \frac{\text{m}}{\text{s}} \cdot 60 \text{ s} \\ s_1 &= 900 \text{ m} \\ \\ s_2 &= \frac12 \cdot 5 \; \frac{\text{m}}{\text{s}} \cdot 10 \text{ s} \\ s_2 &= 25 \text{ m} \\ \\ s_3 &= 5 \; \frac{\text{m}}{\text{s}} \cdot 20 \text{ s} \\ s_3 &= 100 \text{ m} \\ \\ s &= s_1 + s_2 + s_3 \\ s &= 1025 \text{ m} \end{align}Ein alternative Betrachtung erfolgt, indem man die einzelnen Bewegungsabschnitte untersucht:
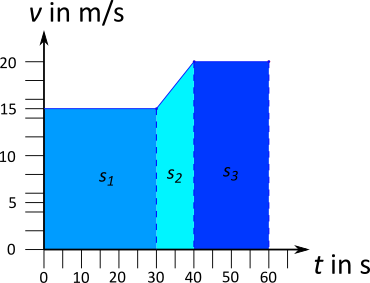
Für den ersten Abschnitt liegt eine gleichförmige Bewegung vor. Die zurückgelegte Strecke lässt sich mit dem folgenden Ansatz bestimmen:
\begin{align} s_1 &= v \cdot t \\ s_1 &= 15 \; \frac{\text{m}}{\text{s}} \cdot 30 \text{ s} \\ s_1 &= 450 \text{ m} \end{align}Der zweite Abschnitt beinhaltet eine beschleunigte Bewegung mit einer Anfangsgeschwindigkeit $v_0$:
\begin{align} s_2 &= \frac12 \cdot a \cdot t^2 + v_0 \cdot t \\ s_2 &= \frac12 \cdot \Delta v \cdot t + v_0 \cdot t \\ s_2 &= \frac12 \cdot 5 \; \frac{\text{m}}{\text{s}} \cdot 10 \text{ s} + 15 \; \frac{\text{m}}{\text{s}} \cdot 10 \text{ s} \\ s_2 &= 175 \text{ m} \end{align}Im dritten Abschnitt liegt wieder eine gleichförmige Bewegung vor:
\begin{align} s_1 &= v \cdot t \\ s_1 &= 20 \; \frac{\text{m}}{\text{s}} \cdot 20 \text{ s} \\ s_1 &= 400 \text{ m} \end{align}Insgesamt wird damit der Weg $s = s_1 + s_2 + s_3 = 1025 \text{ m}$ zurückgelegt.
• Gleichförmige und (mehrere) beschleunigte Bewegung(-en) gleichzeitig
Liegen gleichzeitig mehrere Bewegungszustände vor, u.U. auch mehrere Bewegungszustände der gleichen Art, können alle Zustände einzeln betrachtet werden. Sie überlagern sich ungestört (Superpositionsprinzip).
Eine Kugel rollt auf einer leicht abwärts geneigten Rollbahn. Sie bewegt sich anfangs mit einer konstanten Geschwindigkeit $v_0 = 1,5 \, \frac{\text{m}}{\text{s}}$. Durch die Neigung erfährt sie eine Beschleunigung von $a_1 = 0,5 \; \frac{\text{m}}{\text{s}^2}$. Weil sie aber auf einer Rollbahn rollt, wird sie auch durch die Reibung gebremst. Das wird durch eine zweite Beschleunigung $a_2 = -0,3 \; \frac{\text{m}}{\text{s}^2}$ ausgedrückt. Die Bahn hat insgesamt eine Länge von $s = 3 \text{ m}$, die Kugel startet mit der Anfangsgeschwindigkeit $v_0$ bei $t_0 = 0 \text{ s}$ und $s_0 = 0 \text{ m}$.
Bestimme die zurückgelegte Strecke nach $t_1 = 1,2 \text{ s}$.
Zu welchem Zeitpunkt hat die Kugel das Ende der Rollbahn erreicht?
Bestimme die Geschwindigkeit der Kugel bei $s_1 = 1,5 \text{ m}$ und am Ende der Bahn.
Es gilt der Zusammenhang
$$ s = \frac12 a t^2 + v_0 t + s_0 $$Für die gegebene Aufgabenstellung lautet der Ansatz:
\begin{align} s(t_1) &= \frac12 \cdot a_1 \cdot t_1^2 + \frac12 \cdot a_2 \cdot t_1^2 + v_0 \cdot t_1 \end{align}Da alle Bewegungen unanhängig voneinander vorliegen (die Neigung hängt nicht von der Reibung ab und umgekehrt), können alle Bestandteile, also beide Beschleunigungen und die konstante Geschwindigkeit nacheinander eingesetzt werden. Das führt dann zu
\begin{align} s(1,2 \text{ s}) &= \frac12 \left(0,5 - 0,3 \right) \; \frac{\text{m}}{\text{s}^2} \cdot \left(1,2 \text{ s} \right)^2 + 1,5 \; \frac{\text{m}}{\text{s}} \cdot 1,2 \text{ s} \\ \\ s &= 1,944 \text{ m} \end{align}Für die nächste Aufgabe wird der gleiche Ansatz verfolgt:
$$ s(t) = \frac12 \cdot a_1 \cdot t^2 + \frac12 \cdot a_2 \cdot t^2 + v_0 \cdot t $$Da der zurückgelegte Weg bekannt ist, muss die Gleichung nach $t$ umgestellt werden. Da $t$ aber sowohl linear als auch quadratisch vorkommt, wird hier die $pq-$Formel zur Lösung einer quadratischen Gleichung benötigt. Durch Umstellen erhält man:
\begin{align} 3 \text{ m} &= \frac12 \cdot 0,2 \; \frac{\text{m}}{\text{s}^2} \cdot t^2 + 1,5 \; \frac{\text{m}}{\text{s}} \cdot t \\ \\ 0 &= \frac12 \cdot 0,2 \; \frac{\text{m}}{\text{s}^2} \cdot t^2 + 1,5 \; \frac{\text{m}}{\text{s}} \cdot t - 3 \text{ m} \\ \\ 0 &= t^2 + \frac{1,5 \; \frac{\text{m}}{\text{s}}}{\frac12 \cdot 0,2 \; \frac{\text{m}}{\text{s}^2}} \cdot t - \frac{3 \text{ m}}{\frac12 \cdot 0,2 \; \frac{\text{m}}{\text{s}^2}} \\ \\ 0 &= t^2 + 15 \text{ s} \cdot t - 30 \text{ s}^2 \\ \\ t_{1,2} &= - 7,5 \text{ s} \pm \sqrt{\left(7,5 \text{ s}\right)^2 + 30 \text{ s}^2} \\ \\ t_{1,2} &= - 7,5 \text{ s} \pm \sqrt{86,25 \text{ s}^2} \\ \\ t_1 = - 16,79 \text{ s} \qquad &\vee \qquad t_2 = 1,79 \text{ s} \end{align}Das Ergebnis für $t_1$ ist physikalisch nicht sinnvoll, da es in der Vergangenheit liegt. Die Lösung ist demnach $t = 1,79 \text{ s}$.
Die dritte Aufgabe wird nach den folgenden Ansätzen gelöst:
\begin{align} s &= \frac12 a_1 t^2 + \frac12 a_2 t^2 + v_0 t \\ v &= a_1 t + a_2 t + v_0 \end{align}Hintergrund ist wieder, dass sich die Bewegungszustände ungestört überlagern. Beide Gleichungen werden etwas kompakter notiert:
\begin{align} s &= \frac12 (a_1 + a_2) t^2 + v_0 t \\ \\ v &= (a_1 + a_2) t + v_0\\ t &= \frac{v - v_0}{(a_1 + a_2)} \end{align}Einsetzen führt zu
\begin{align} s &= \frac12 (a_1 + a_2) \left(\frac{v - v_0}{(a_1 + a_2)}\right)^2 + v_0 \frac{v - v_0}{(a_1 + a_2)} \\ \\ s &= \frac{(v - v_0)^2}{2(a_1 + a_2)} + \frac{v_0 (v - v_0)}{(a_1 + a_2)} \end{align}An dieser Stelle müssen erstmal die beiden Brüche bearbeitet werden:
\begin{align} s &= \frac{(v - v_0)^2}{2(a_1 + a_2)} + \frac{v_0 (v - v_0)}{(a_1 + a_2)} \\ \\ s &= \frac{(v - v_0)^2}{2(a_1 + a_2)} + \frac{2v_0 (v - v_0)}{2(a_1 + a_2)} \\ \\ s &= \frac{(v^2 - 2vv_0 + v_0^2)}{2(a_1 + a_2)} + \frac{(2vv_0 - 2v_0^2)}{2(a_1 + a_2)} \\ \\ s &= \frac{v^2 - 2vv_0 + v_0^2 + 2vv_0 - 2v_0^2}{2(a_1 + a_2)} \\ \\ s &= \frac{v^2 - v_0^2}{2(a_1 + a_2)} \end{align}Auflösen nach $v$:
\begin{align} 2s(a_1 + a_2) &= v^2 - v_0^2 \\ \\ 2s(a_1 + a_2) + v_0^2 &= v^2 \\ \\ v &= \sqrt{2s(a_1 + a_2) + v_0^2} \\ \\ v &= \sqrt{2 \cdot 1,5 \text{ m} \cdot 0,2 \; \frac{\text{m}}{\text{s}^2} + \left(1,5 \; \frac{\text{m}}{\text{s}}\right)^2} \\ \\ v &= 1,69 \; \frac{\text{m}}{\text{s}} \end{align}Das ist die Geschwindigkeit bei $s = 1,5 \text{m}$. Mit der gleichen Formel wird auch die Geschwindigkeit bei $s = 3 \text{ m}$ bestimmt:
\begin{align} v &= \sqrt{2 \cdot 3 \text{ m} \cdot 0,2 \; \frac{\text{m}}{\text{s}^2} + \left(1,5 \; \frac{\text{m}}{\text{s}}\right)^2} \\ \\ v &= 1,86 \; \frac{\text{m}}{\text{s}} \end{align}| gleichförmige Bewegung | ||
| Randbedingungen | $s_0 = 0$ $v_0 = \text{ konstant}$ $v_0 > 0$ | $s_0 \neq 0$ $v_0 = \text{ konstant}$ $v_0 > 0$ |
| Zeit-Weg-Gesetz | $s(t)=v \cdot t$ | $s(t)=v \cdot t + s_0$ |
| t-s-Diagramm |  |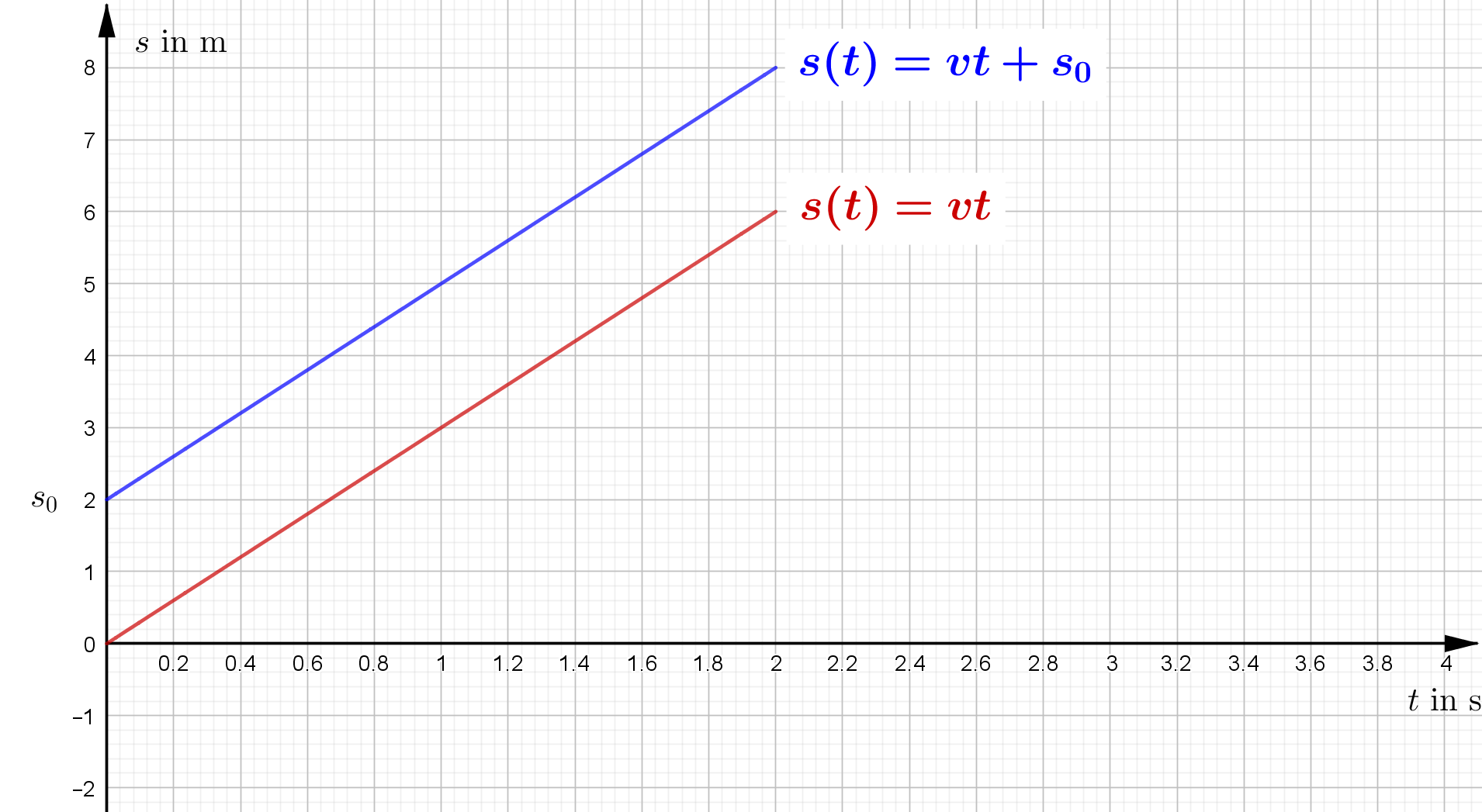
|
| Zeit-Geschwindigkeit-Gesetz | $v(t)=v_0$ | |
| t-v-Diagramm |  |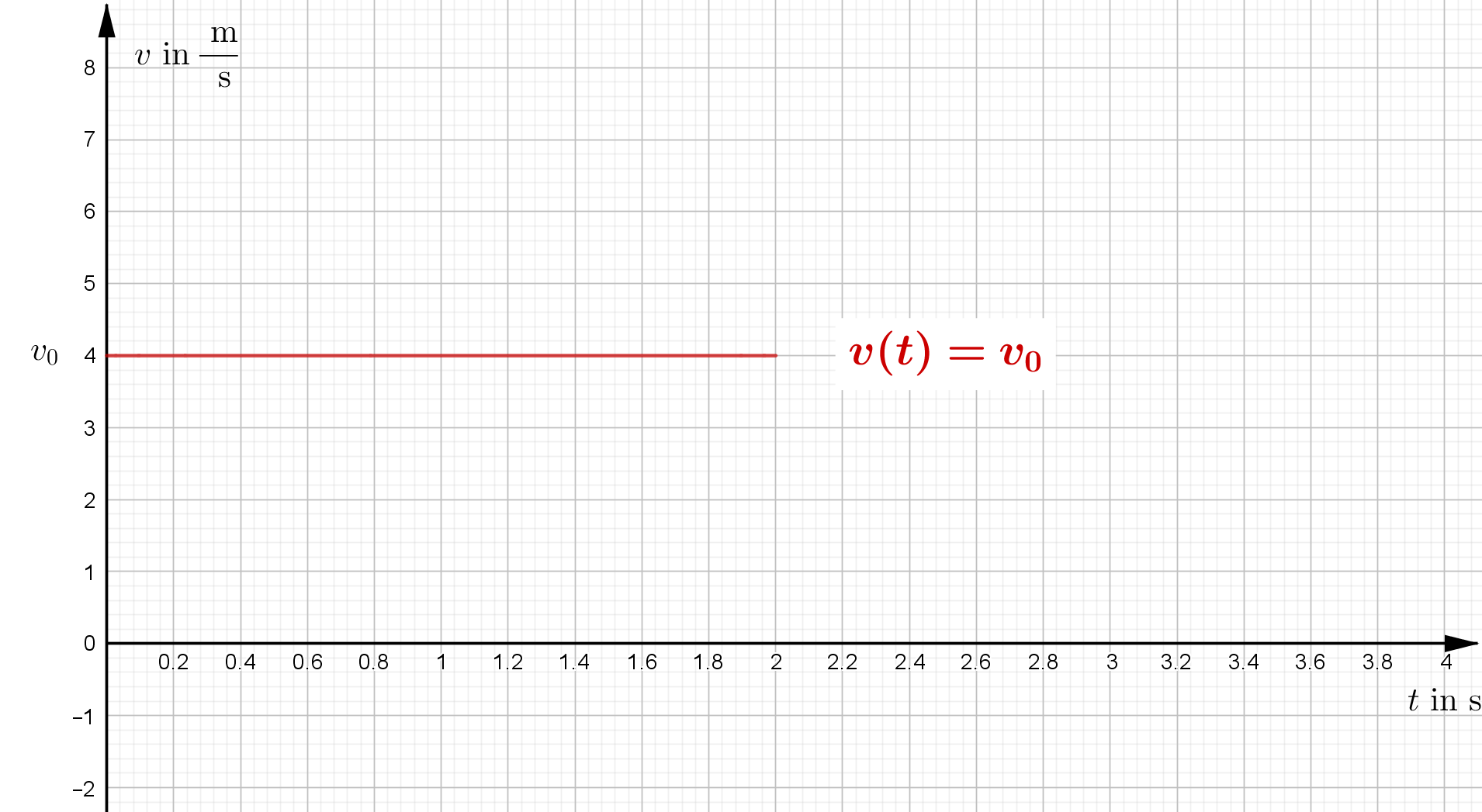
|
| Zeit-Beschleunigung-Gesetz | $a(t)=0$ | |
| t-a-Diagramm |  |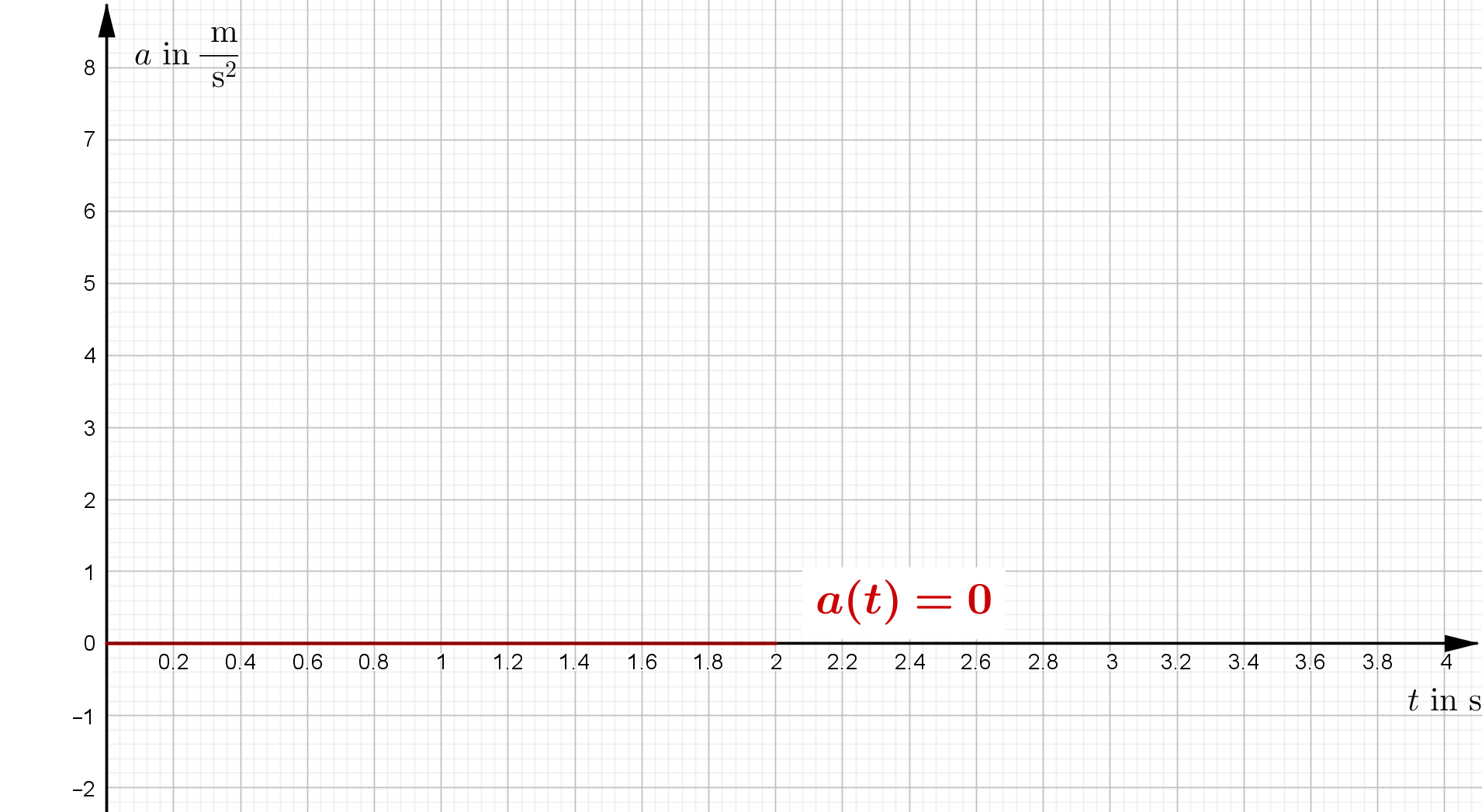
|
| konstant beschleunigte Bewegung | |||
| Randbedingungen | $s_0 = 0$ $v_0 = 0$ $a > 0$ | $s_0 \neq 0$ $v_0 = 0$ $a > 0$ | $s_0 \neq 0$ $v_0 \neq 0$ $a > 0$ |
| Zeit-Weg-Gesetz | $s(t)=\frac12 \cdot a \cdot t^2$ | $s(t)=\frac12 \cdot a \cdot t^2 + s_0$ | $s(t)=\frac12 \cdot a \cdot t^2 + v_0 \cdot t + s_0$ |
| t-s-Diagramm |  |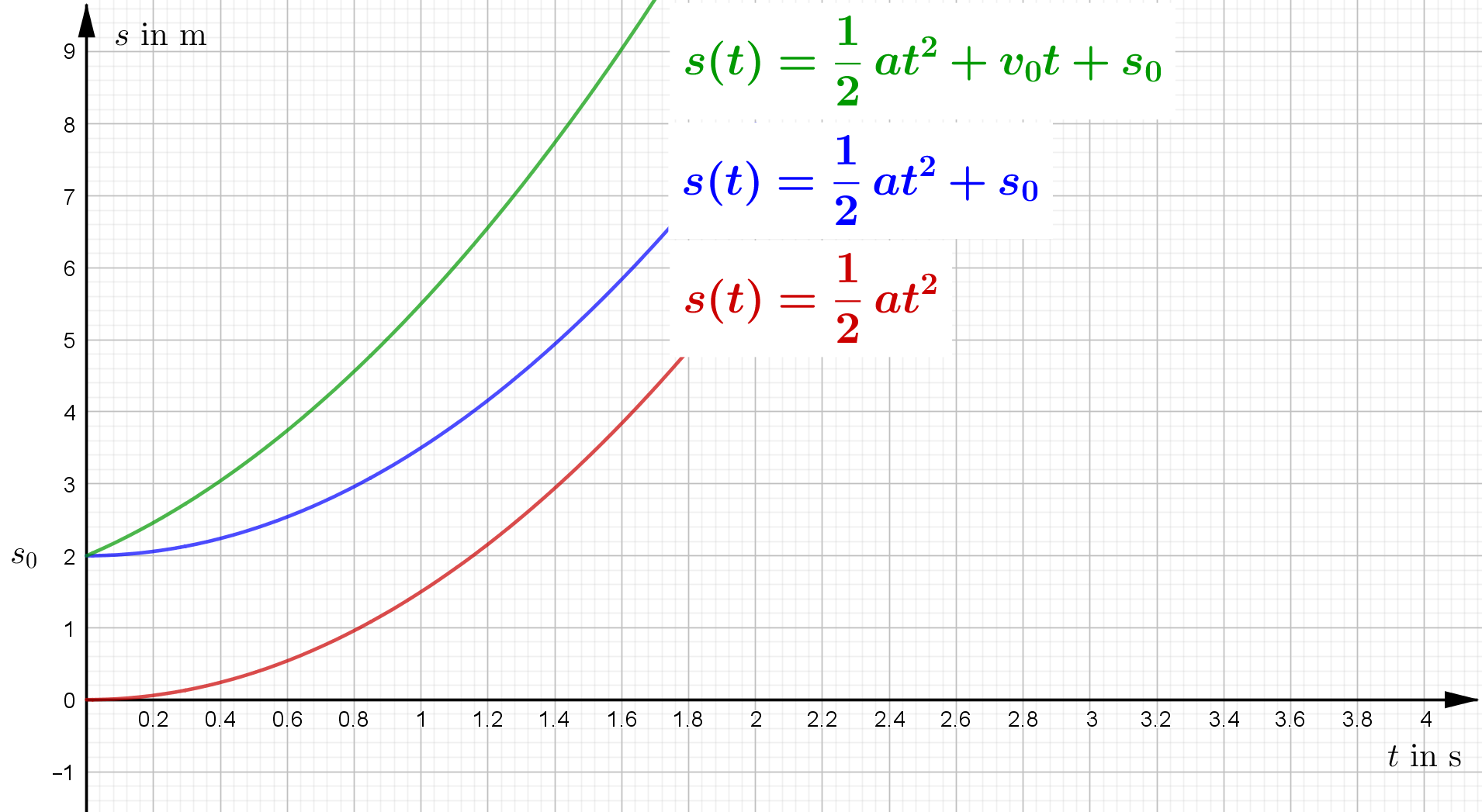
||
| Zeit-Geschwindigkeit-Gesetz | $v(t)=a \cdot t$ | $v(t)=a \cdot t + v_0$ | |
| t-v-Diagramm |  |
||
| Zeit-Beschleunigung-Gesetz | $a(t)=a$ | ||
| t-a-Diagramm |  |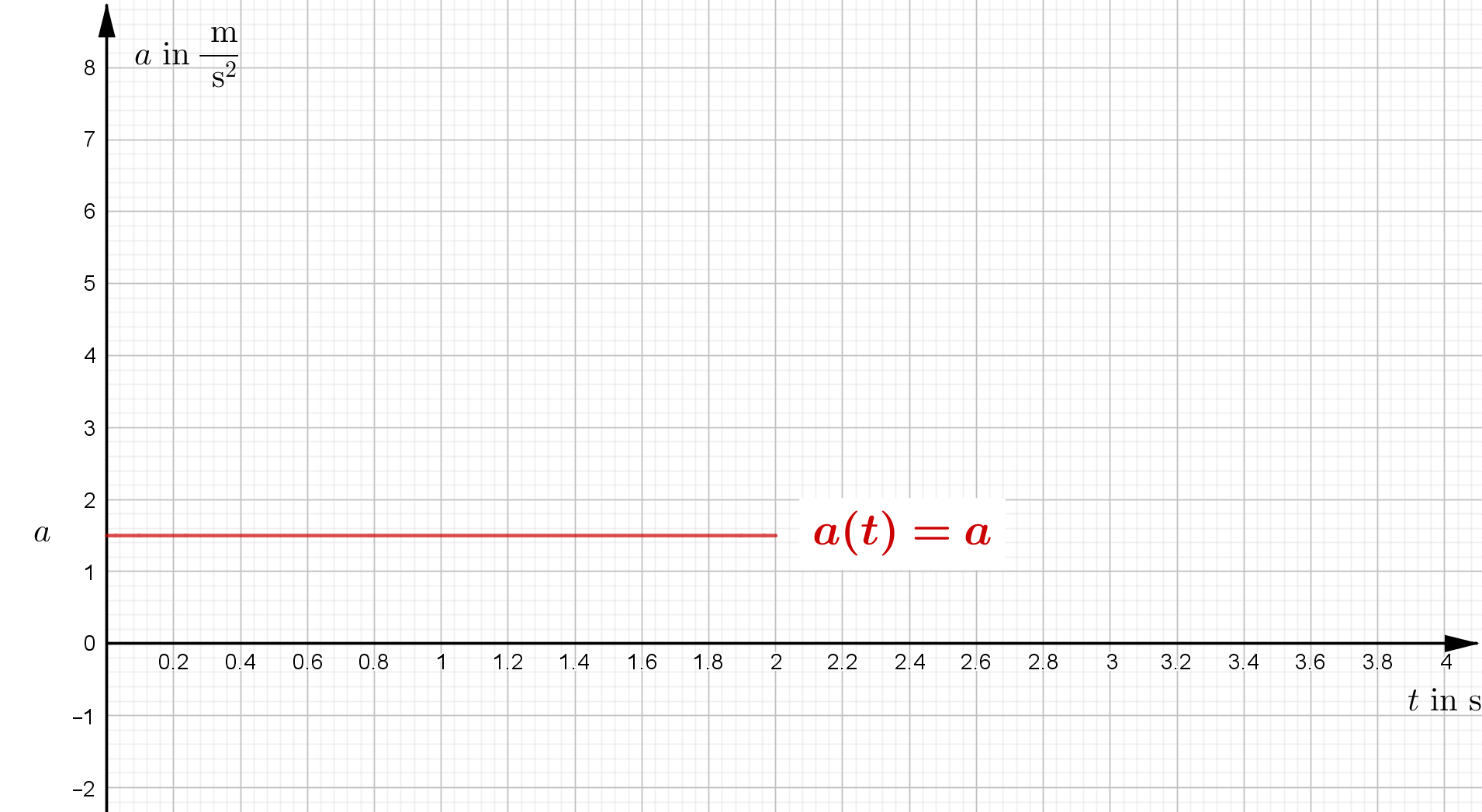
||
Die Fall- und Wurfbewegungen sind Sonderfälle einzelner Bewegungen oder der Überlagerung einzelner Bewegungen.
Der freie Fall ist ein Spezialfall der gleichmäßig beschleunigten Bewegung.
Der senkrechte Wurf ist die überlagerung gleichförmiger Bewegung mit dem freien Fall, wenn die gleichförmige Bewegung auf der selben
Wirkungslinie erfolgt wie der freie Fall. Dabei gibt es die Unterscheidung, ob die gleichförmige Bewegung parallel oder antiparallel zum
freien Fall erfolgt.
Der waagerechte Wurf liegt dann vor, wenn die gleichförmige Bewegung senkrecht zum freien Fall erfolgt.
Erfolgt die gleichförmige Bewegung allgemein in irgendeine Richtung, spricht man vom schiefen Wurf.
Lässt man einen Körper aus unterschiedlichen Höhen fallen und misst die Zeit, bis der Körper auf dem Boden ankommt, kann man die Beschleunigung
bestimmen, mit der sich der Körper in Richtung „unten“ bewegt. Mit der Festlegung, dass die Anfangsgeschwindigkeit $v_0 = 0 \; \frac{\text{m}}{\text{s}}$ ist
und die Bewegung bei $s_0 = 0 \; \text{m}$ beginnt, folgt der formale Zusammenhang:
$$
s = \frac{1}{2} a t^2
$$
Beispiel:
| Strecke $s$ in m |
Zeit $t$ in s |
$t^2$ in s2 |
|---|---|---|
|
0,45 0,40 0,35 0,30 0,25 0,20 0,15 0,10 0,05 0 |
0,3104 0,2934 0,2752 0,2558 0,2350 0,2124 0,1868 0,1576 0,1212 0 |
0,0963 0,0861 0,0757 0,0654 0,0552 0,0451 0,0349 0,0248 0,0147 0 |
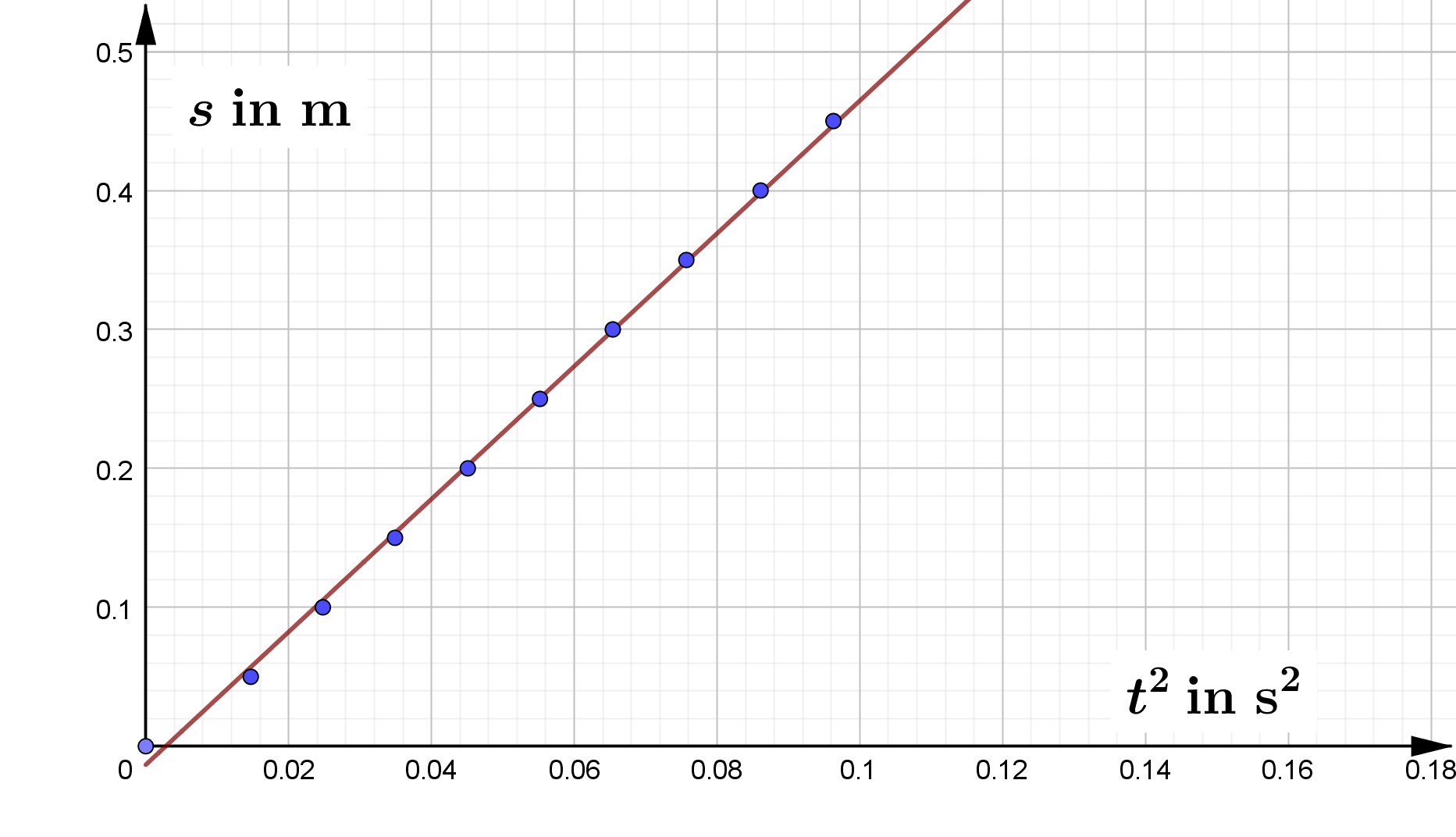
Zur Herkunft des Wertes für $g$, siehe den Bereich Gravitationskraft.
Der römische Dichter und Philosoph Lukrez beschrieb schon ca. 55 v. Chr. in seinem Werk „De rerum natura” („Über die Natur der Dinge”), dass fallende Objekte nur vom Wasser- oder Luftwiderstand gebremst werden, und daher leichte Körper langsamer, im Vakuum aber alle Körper gleich schnell fallen müssen:
Wer nun etwa vermeint, die schwereren Körper, die senkrecht
Rascher im Leeren versinken, vermöchten von oben zu fallen
Auf die leichteren Körper und dadurch die Stöße bewirken,
Die zu erregen vermögen die schöpferisch tätigen Kräfte:
Der entfernt sich gar weit von dem richtigen Wege der Wahrheit.
Denn was immer im Wasser herabfällt oder im Luftreich,
Muß, je schwerer es ist, um so mehr sein Fallen beeilen,
Deshalb, weil die Natur des Gewässers und leichteren Luftreichs
Nicht in der nämlichen Weise den Fall zu verzögern imstand ist,
Sondern im Kampfe besiegt vor dem Schwereren schneller zurückweicht:
Dahingegen vermöchte das Leere sich niemals und nirgends
Wider irgendein Ding als Halt entgegenzustellen,
Sondern es weicht ihm beständig, wie seine Natur es erfordert.
Deshalb müssen die Körper mit gleicher Geschwindigkeit alle
Trotz ungleichem Gewicht durch das ruhende Leere sich stürzen (...)
Erst Robert Boyle bestätigte 1659 experimentell, dass Körper unterschiedlicher Masse im Vakuum gleich schnell fallen.
Die wesentliche Grundlage für die Möglichkeit, solche Probleme wie den waagerechten Wurf bearbeiten zu können, ist die Erkenntnis, dass sich Bewegungen unabhängig voneinander überlagern können. Das wird durch das nachfolgende Video demonstriert:
Die unabhängige Überlagerung bedeutet, dass jede beliebige Bewegung als zwei Bewegungen in eine x-Richtung und in eine y-Richtung
aufgefasst werden kann.
Um das tun zu können muss zunächst ein Koordinatensystem vorgegeben werden, wobei der Ursprung frei wählbar ist. Allerdings gibt es
natürlich sinnvolle Möglichkeiten für die Wahl des Ursprungs und weniger sinnvolle. Die Folge von weniger sinnvollen Positionen
ist aber nur, dass es etwas mehr Rechenaufwand bedarf um zu Lösungen zu kommen.
Beispiel für einen waagerechten Wurf
Eine solche Bewegung wird durchgeführt, wenn sich ein Körper mit einer konstanten horizontalen Geschwindigkeit im Schwerefeld der Erde bewegt. Das ist z.B. der Fall, wenn ein Objekt von einer Tischoberfläche gestoßen wird, wenn ein Wasserstrahl aus einem waagerecht gehaltenen Schlauch austritt oder wenn etwas aus einem fliegenden Flugzeug fallen gelassen wird.
Analyse der Bewegungen
Zunächst zur Bewegung in x-Richtung (waagerecht):
Hierbei handelt es sich um eine gleichförmige Bewegung, da der Körper sich mit einer konstanten Geschwindigkeit in x-Richtung bewegt und keine weiteren Kräfte in dieser Richtung auf ihn einwirken. Es gilt also: \begin{align} s_x &= v_x \cdot t \\ v_x &= v_0 \\ a_x &= 0 \end{align}
Zur Bewegung in y-Richtung (senkrecht):
Die Bewegung in y-Richtung ist eine Bewegung mit einer konstanten Beschleunigung, der Fallbeschleunigung. Es gelten die Gesetze des freien Falls: \begin{align} s_y &= - \frac{1}{2} \cdot a_y \cdot t^2 \\ v_y &= - \, a_y \cdot t \\ a_y &= g \end{align}
Woher kommen die Minuszeichen? Die kommen daher, weil ein sinnvolles Koordinatensystem seinen Ursprung in der Abwurfstelle hat. Die Bewegung nach unten, also die konstant beschleunigte Bewegung, erfolgt in die negative y-Richtung, da ein kartesisches Koordinatensystem immer so aufgebaut ist, dass die y-Achse nach oben weist, wenn die x-Achse nach rechts zeigt.
Skizze
Für die Wurfweite gilt: $s_x = v_0 \cdot t$ und für die Abwurfhöhe: $s_y = - \frac 12 \cdot g \cdot t^2$
Aufstellen der Parabelgleichung
Setzt man $s_x = x$ und $s_y = y$ folgt: \begin{align} x &= v_0 \cdot t \\ t &= \frac{x}{v_0} \\ \\ y &= - \frac 12 \cdot g \cdot t^2 \\ y &= - \frac 12 \cdot g \cdot \left( \frac{x}{v_0} \right)^2 \\ y &= - \frac 12 \cdot \frac{g}{v_0^2} \cdot x^2 \end{align}
Beispielaufgabe
Anatoly Timoschtschuk, ehemaliger Spieler des FC Bayern München, hat am 14.Mai 2011 mit 134,3 km/h eine Rekord-Schussgeschwindigkeit
im Fussball erreicht (Quelle). Angenommen, er schafft das noch einmal und schießt einen am Rande einer 10 m hohen Klippe liegenden Ball
waagerecht mit eben derselben Geschwindigkeit nach vorn.
Berechne die Stelle, an der der Ball den Boden berührt. Bestimme die Flugzeit des Balls. Gib an, unter welchem Winkel der Ball auf
dem Boden aufkommt.
Zunächst muss die Geschwindigkeit in die richtige Einheit umgerechnet werden:
$$
134 \frac{\text{km}}{\text{h}} = \frac{134}{3,6} \frac{\text{m}}{\text{s}} = 37,22 \frac{\text{m}}{\text{s}}
$$
Es gilt:
\begin{align}
y &= - \frac 12 \cdot g \cdot t^2 \\
t &= \sqrt{\frac{2 y}{g}} \\
t &= \sqrt{\frac{2 \cdot 10 \text{ m}}{9,81 \frac{\text{m}}{\text{s}^2}}} \\
t &= 1,428 \text{ s}
\end{align}
Berücksichtigt wurde hier u.a., dass die Höhe der Klippe über dem Boden gleich der Tiefe des Bodens unter der Klippe ist. Damit
ist $y = - 10 \text{ m}$. Weiterhin wurde die zweite Lösung für die Quadratwurzel, hier die negative, vernachlässigt, da sie
physikalisch sinnlos ist.
Mit der jetzt bekannten Zeit lässt sich die Schussweite bestimmen:
\begin{align}
x &= v_0 \cdot t \\
x &= 37,22 \frac{\text{m}}{\text{s}} \cdot 1,428 \text{ s} \\
x &= 53,15 \text{ m}
\end{align}
Der Auftreffwinkel lässt sich mit Hilfe der Parabelgleichung bestimmen:
\begin{align}
y &= - \frac 12 \cdot \frac{g}{v_0^2} \cdot x^2 \\
y &= - \frac 12 \cdot \frac{9,81 \frac{\text{m}}{\text{s}^2}}{\left( 37,22 \frac{\text{m}}{\text{s}} \right)^2} \cdot x^2 \\
y &= -0,00354 \text{ m}^{-1} \cdot x^2
\end{align}
Der Winkel ergibt sich aus der Steigung der Parabel an der Stelle $x = 53,15 \text{ m}$. Es folgt:
\begin{align}
m &= \frac{dy}{dx} = - 0,00708 \text{ m}^{-1} \cdot x = - 0,00708 \text{ m}^{-1} \cdot 53,15 \text{ m} \\
m &= - 0,3763 \\ \\
\alpha &= arctan (- 0,3763) \\
\alpha &= - 20,62 °
\end{align}
Der Auftreffwinkel beträgt also 20,62° bei einer Entfernung von 53,15 m von der Klippe. Die Flugzeit beträgt 1,43 s.
Analog zum waagerechten Wurf wird die Bewegung in zwei Teilbewegungen unterteilt. Allerdings erfolgen beim senkrechten Wurf beide Teilbewegungen in $y-$Richtung. In $x-$Richtung gibt es keine Bewegung.
Zunächst gibt es die gleichförmige Bewegung in $y-$Richtung, d.h. nach oben, und anschließend die beschleunigte Bewegung des freien Falls in $-y-$Richtung, d.h. nach unten. Wenn beim senkrechten Wurf die Wurfbewegung in dieselbe Richtung wie die Fallbewegung erfolgt, addieren sich beide Bewegungen in $-y-$Richtung.
Für die gleichförmige Wurfbewegung gilt: $$ s_y = v_{y,0} \cdot t $$ Die Fallbewegung kann so beschrieben werden: $$ s_y = - \frac12 g \cdot t^2 $$ Insgesamt ergibt sich für die Bewegung in $y-$Richtung: $$ s_y = - \frac12 g \cdot t^2 + v_{y,0} \cdot t $$ Für die Geschwindigkeit in $y-$Richtung gilt: $$ v_y = - g \cdot t + v_{y,0} $$
Beispielaufgabe 1
Feuerwerksraketen werden vom Boden nach oben geschossen und kommen irgendwann wegen der Schwerkraft wieder auf dem Boden an. Für Grossfeuerwerke werden u.a. sogenannte Kugelbomben aus einer Röhre nach oben geschossen. Dabei werden Abschussgeschwindigkeiten von bis zu 110 Metern pro Sekunde erreicht.
Berechne die Dauer des Flugs bis zum Auftreffen auf dem Boden.
Bestimme die erreichbare Höhe.
Berechne die Auftreffgeschwindigkeit.
Zunächst gilt die Formel
$$s_y = - \frac12 g t^2 + v_0 t + s_0$$$g$ ist die Fallbeschleunigung mit $g = 9,81 \; \frac{\text{m}}{\text{s}^2}$, $v_0$ die Abschussgeschwindigkeit mit $v_0 = 110 \; \frac{\text{m}}{\text{s}}$ und $s_0$ die Höhe, aus der der Abschuss erfolgt. Dafür wird ein Wert von $s_0 = 0,5 \text{ m}$ angenommen. Es folgt also:
$$ s_y = - \frac12 \cdot 9,81 \; \frac{\text{m}}{\text{s}^2} \cdot t^2 + 110 \; \frac{\text{m}}{\text{s}} \cdot t + 0,5 \text{ m} $$
Der Flug bis zum Wiederauftreffen auf dem Boden wird durch die Flugparabel beschrieben. Der Zeitpunkt den Auftreffens wird durch die zweite Nullstelle der Parabel bestimmt. Die erreichbare Höhe kann durch die Bestimmung des Scheitelpunkts der Parabel gefunden werden. Die Geschwindigkeit wird durch den folgenden Ansatz bestimmbar: $v = - gt + v_0$. Dafür wird die Zeit benötigt, die aber mit der Bestimmung der Nullstelle bekannt ist.
\begin{align} s_y &= 0 \\ \\ 0 &= - \frac12 \cdot 9,81 \; \frac{\text{m}}{\text{s}^2} \cdot t^2 + 110 \; \frac{\text{m}}{\text{s}} \cdot t + 0,5 \text{ m} \\ \\ 0 &= t^2 - \frac{2 \cdot 110 \; \frac{\text{m}}{\text{s}}}{9,81 \; \frac{\text{m}}{\text{s}^2}} \cdot t - \frac{2 \cdot 0,5 \text{ m}}{9,81 \; \frac{\text{m}}{\text{s}^2}} \\ \\ t_{1,2} &= \frac{110 \; \frac{\text{m}}{\text{s}}}{9,81 \; \frac{\text{m}}{\text{s}^2}} \pm \sqrt{\left(\frac{110 \; \frac{\text{m}}{\text{s}}}{9,81 \; \frac{\text{m}}{\text{s}^2}}\right)^2 + \frac{2 \cdot 0,5 \text{ m}}{9,81 \; \frac{\text{m}}{\text{s}^2}}} \\ \\ t_1 &= - 0,0045 \text{ s} \\ t_2 &= 22,43 \text{ s} \end{align}Die Nullstelle der Parabel liegt also bei $t = 22,43 \text{ s}$. Die Nullstelle im negativen Bereich ist für den Sachzusammenhang nicht relevant.
Für den Scheitelpunkt könnte die Scheitelpunktform genutzt werden. Da diese aber durch eine mehr oder weniger schwierige Umformung ermittelt werden muss, wird hier eine einfachere Methode durchgeführt. Die Parabel ist symmetrisch bezüglich einer senkrechten Achse durch den Scheitelpunkt. Insbesondere sind die beiden Nullstellen gleich weit von der x-Koordinate des Scheitelpunkts entfernt. Dieser ergibt sich also aus dem Term $- \frac{p}{2}$ aus der pq-Formel.
Damit ist die x-Koordinate des Scheitelpunkts $$\frac{110 \; \frac{\text{m}}{\text{s}}}{9,81 \; \frac{\text{m}}{\text{s}^2}} = 11,21 \text{ s}$$
Die y-Koordinate wird durch Einsetzen ermittelt: $$s_y = - \frac12 \cdot 9,81 \; \frac{\text{m}}{\text{s}^2} \cdot \left(11,21 \text{ s}\right)^2 + 110 \; \frac{\text{m}}{\text{s}} \cdot 11,21 \text{ s} + 0,5 \text{ m}$$ $$ s_y = 617,22 \text{ m}$$
Für die Geschwindigkeit folgt:
\begin{align} v &= - 9,81 \; \frac{\text{m}}{\text{s}^2} \cdot 22,43 \text{ s} + 110 \; \frac{\text{m}}{\text{s}} \\ \\ v &= - 110,04 \; \frac{\text{m}}{\text{s}} \end{align}Beispielaufgabe 2
Beim Tennis-Aufschlag ist es wichtig, den Ball so nach oben zu werfen, dass man ihn mit dem Schläger möglichst weit oben trifft, um den besten Winkel für die Flugbahn des Balles ins gegnerische Feld zu haben. Ein 1,80 m großer Spieler wirft den Ball etwa in Kopfhöhe mit einer Geschwindigkeit von $v_{y,0} \frac{\text{m}}{\text{s}}$ nach oben. Es gilt also insgesamt: $$ s_y = - \frac12 \cdot 9,81 \; \frac{\text{m}}{\text{s}^2} \cdot t^2 + v_{y,0} \; \frac{\text{m}}{\text{s}} \cdot t $$ Wenn nun der Spieler in der Lage ist, den Ball in einer Höhe von 1,50 m über dem Kopf zu treffen, kann man nun die Zeit bestimmen, die der Spieler hat, um die Ausholbewegung mit dem Schläger zu machen. Mit $s_y = 1,50 \; \text{m}$ folgt: \begin{align} 1,50 \; \text{m} &= - \frac12 \cdot 9,81 \; \frac{\text{m}}{\text{s}^2} \cdot t^2 + v_{y,0} \; \frac{\text{m}}{\text{s}} \cdot t \\ \\ 0 &= - \frac12 \cdot 9,81 \; \frac{\text{m}}{\text{s}^2} \cdot t^2 + v_{y,0} \; \frac{\text{m}}{\text{s}} \cdot t - 1,50 \; \text{m} \end{align} Das ist eine quadratische Gleichung mit den Lösungen: $$ t_{1,2} = \frac{v_{y,0}}{9,81 \; \frac{\text{m}}{\text{s}^2}} \pm \sqrt{\left( \frac{v_{y,0}}{9,81 \; \frac{\text{m}}{\text{s}^2}} \right)^2 - \frac{1,50 \; \text{m}}{4,905}} $$ Es gibt ausschließlich Lösungen, wenn der Term unter der Wurzel größer oder gleich Null ist. Es folgt also für die Abwurfgeschwindigkeit: $$ v_{y,0} \ge 9,81 \cdot \sqrt{\frac{1,5}{4,905}} $$ Mit einem gegebenen Wert für die Abwurfgeschwindigkeit kann die quadratische Gleichung gelöst werden.
Es ergeben sich zwei Lösungen, die beide aussagen, zu welchen Zeitpunkten der Bewegung der Ball sich in einer Höhe von 1,50 m über dem Kopf des Spielers befindet. Der erste Zeitpunkt ist derjenige bei der Aufwärtsbewegung, der zweite derjenige bei der Abwärtsbewegung.
Der schiefe Wurf zeichnet sich dadurch aus, dass der freie Fall in $-y-$Richtung überlagert wird durch eine gleichförmige Bewegung in $x-$ und $y-$Richtung. Diese muss also aufgeteilt werden in die Anteile, die genau in die $x-$Richtung und genau in die $y-$Richtung weisen.
Der Anteil in $x-$Richtung ist: $$v_x = v \cdot \cos \alpha$$ und für die $y-$Richtung gilt: $$v_y = v \cdot \sin \alpha$$
In der weiteren Bearbeitung folgt nun eine Überlagerung von waagerechtem und senkrechtem Wurf. Die Bewegung in $x-$Richtung ist weiterhin ausschließlich eine gleichförmige Bewegung, die in $y-$Richtung ist eine gleichförmige Bewegung in die positive Richtung und ein freier Fall in die negative Richtung.
Damit folgen die Bewegungsgleichungen
\begin{align} s_x &= v \cdot \cos \alpha \cdot t \\ \\ s_y &= - \frac12 g \cdot t^2 + v \cdot \sin \alpha \cdot t + s_{y,0} \\ \\ \\ v_x &= v \cdot \cos \alpha \\ \\ v_y &= - g \cdot t + v \cdot \sin \alpha \end{align}Beispielaufgabe
Ein Tennisball wird im Winkel von 30° zur Horizontalen mit einer Anfangsgeschwindigkeit von 20 m/s aus einer Höhe von 5 m abgeworfen.
Bestimme die Wurfdauer, die Wurfhöhe und die Wurfweite sowie die Bahngleichung des Wurfs. Unter welchem Winkel müsste geworfen werden, damit die Wurfweite maximal wird?
Für die Wurfdauer ist entscheidend, für welches $t$ der Wert $s_y = 0$ wird. Also folgt
\begin{align} s_y &= - \frac12 g \cdot t^2 + v \cdot \sin \alpha \cdot t + s_{y,0} \\ \\ s_y &= - \frac12 9,81 \; \frac{\text{m}}{\text{s}^2} \cdot t^2 + 20 \; \frac{\text{m}}{\text{s}} \cdot \sin 30° \cdot t + 5 \text{ m} \\ \\ 0 &= t^2 - \frac{2 \cdot 20 \; \frac{\text{m}}{\text{s}} \cdot \sin 30° }{9,81 \; \frac{\text{m}}{\text{s}^2}} - \frac{2 \cdot 5 \text{ m}}{9,81 \; \frac{\text{m}}{\text{s}^2}} \\ \\ t_{1,2} &= \frac{20 \; \frac{\text{m}}{\text{s}} \cdot \sin 30° }{9,81 \; \frac{\text{m}}{\text{s}^2}} \pm \sqrt{\left(\frac{20 \; \frac{\text{m}}{\text{s}} \cdot \sin 30° }{9,81 \; \frac{\text{m}}{\text{s}^2}}\right)^2 + \frac{2 \cdot 5 \text{ m}}{9,81 \; \frac{\text{m}}{\text{s}^2}}} \\ \\ t_1 &= - 0,42 \text{ s} \\ \\ t_2 &= 2,45 \text{ s} \end{align}Für die Wurfhöhe kann ausgenutzt werden, dass der Scheitelpunkt einer Parabel genau in der Mitte zwischen den beiden Nullstellen ist. Mit anderen Worten ist die $x-$Koordinate des Scheitelpunkts genau der Term $- \left(\frac{p}{2}\right)$ aus der pq-Formel für die Nullstellen.
\begin{align} t_{\text{Scheitelpunkt}} &= \frac{20 \; \frac{\text{m}}{\text{s}} \cdot \sin 30°}{9,81 \; \frac{\text{m}}{\text{s}^2}} \\ t_{\text{Scheitelpunkt}} &= 1,02 \text{ s} \\ \\ s_y &= - \frac12 9,81 \; \frac{\text{m}}{\text{s}^2} \cdot \left(1,02 \text{ s}\right)^2 + 20 \; \frac{\text{m}}{\text{s}} \cdot \sin 30° \cdot 1,02 \text{ s} + 5 \text{ m} \\ \\ s_y &= 10,1 \text{ m} \end{align}Für die Weite ist der $s_x-$Wert gefragt, bei dem $s_y = 0$ gilt, also $s_x$ zum Zeitpunkt $t = 2,45 \text{ s}$.
\begin{align} s_x &= v \cdot \cos \alpha \cdot t \\ \\ s_x &= 20 \; \frac{\text{m}}{\text{s}} \cdot \cos 30° \cdot 2,45 \text{ s} \\ \\ s_x &= 42,44 \text{ m} \end{align}Die Bahngleichung bekommt man, indem die Gleichung für $s_x$ in die Gleichung für $s_y$ eingesetzt wird.
\begin{align} s_x &= v \cdot \cos \alpha \cdot t \qquad \rightarrow t = \frac{s_x}{v \cdot \cos \alpha} \\ \\ s_y &= - \frac12 g \cdot t^2 + v \cdot \sin \alpha \cdot t + s_{y,0} \\ \\ \\ s_y &= - \frac12 g \cdot \left(\frac{s_x}{v \cdot \cos \alpha}\right)^2 + v \cdot \sin \alpha \cdot \frac{s_x}{v \cdot \cos \alpha} + s_{y,0} \\ \\ s_y &= - \frac{g}{2 \cdot v^2 \cdot \cos^2 \alpha} \cdot s_x^2 + \tan \alpha \cdot s_x + s_{y,0} \\ \\ s_y &= - \frac{9,81 \; \frac{\text{m}}{\text{s}^2}}{2 \cdot 400 \; \frac{\text{m}^2}{\text{s}^2} \cdot \cos^2 30° } \cdot s_x^2 + \tan 30° \cdot s_x + 5 \text{ m} \\ \\ s_y &= - 0,016 \cdot s_x^2 + 0,577 \cdot s_x + 5 \end{align}Das ist die Bahngleichung, die als Graph folgendes Aussehen hat:
Für die maximale Wurfweite soll zunächst eine Lösungsidee entwickelt werden. Die Wurfweite ist die zweite Lösung bei der Bestimmung der Nullstellen der Bahngleichung. Diese hängt im vorliegenden Fall von dem Abwurfwinkel $\alpha$ ab, der bis jetzt 30° betrug. Diese Abhängigkeit führt wieder zu einer Funktion, von der dann das Maximum bestimmt werden muss.
Zunächst eine Darstellung der verschiedenen Graphen der Bahngleichungen:
Ein genauerer Blick auf die zweite Nullstelle:
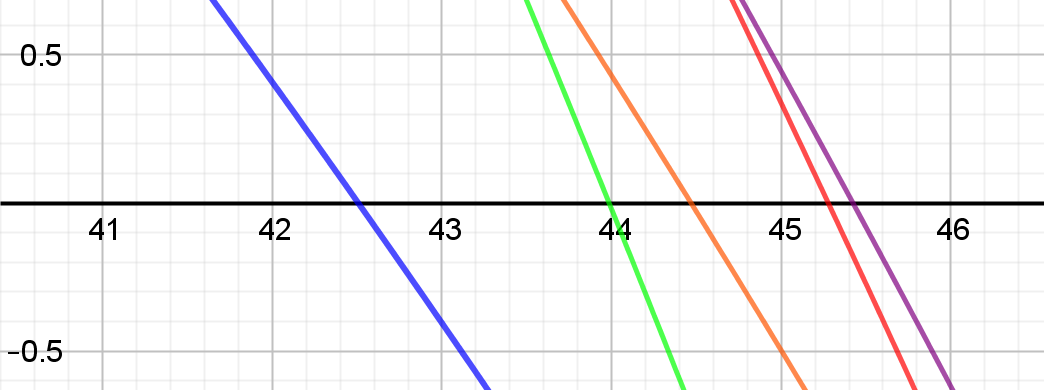
Die Nullstellenbestimmung der Bahngleichung führen zu dem folgenden Ergebnis:
$$ x = \frac{\sin \alpha \cdot \cos \alpha \cdot 400}{9,81} + \sqrt{\frac{\sin^2 \alpha \cdot \cos^2 \alpha \cdot 160000}{9,81^2} + \frac{4000 \cdot \cos^2 \alpha}{9,81}} $$Das ist die Gleichung für die zweite Nullstelle in Abhängigkeit des Winkels $\alpha$. Betrachtet man diese Gleichung als Funktion $x(\alpha)$, erhält man einen Graphen mit einem Maximum bei $\alpha = 41,86°$ und der Wurfweite $x_{max} = 45,5 \text{ m}$.
Hier ist zu beachten, dass die Skalierung der x-Achse im Bogenmaß vorliegt. Für die Umrechnung ins Gradmaß wird der Zahlenwert (hier ca. 0,73) mit 180° multipliziert und durch $\pi$ geteilt:
$$ \frac{0,73 \cdot 180°}{\pi} = 41,83° $$Analog zu der Bewegung entlang einer Linie wird zunächst die Bewegung auf einer Kreisbahn beschrieben. Dafür sind einige neue und zusätzliche Begriffe und Größen notwendig. Die Ursache einer Kreisbewegung soll im Anschluss erläutert werden (Zentripetalkraft).
Neben dem Begriff Zeit t werden die weiteren Größen aus der geradlinigen Bewegung etwas verändert dargestellt. Die Strecke s
bleibt häufig einfach die Strecke s, in manchen Fällen wird die bei einer Kreisbewegung zurückgelegte Strecke auch Bogen oder
Kreisbogen b genannt. Die Geschwindigkeit v wird meist als Bahngeschwindigkeit bezeichnet, ebenso die
Beschleunigung a als Bahnbeschleunigung.
Neue Größen oder Bezeichnungen sind der Radius r der Kreisbahn, die Dauer einer Bewegung auf einem Vollkreis, Umlaufzeit T,
die Anzahl von Umläufen pro Sekunde, Frequenz f, sowie die Strecke für einen Umlauf, den Umfang U.
Zunächst soll noch eine kleine Einschränkung gemacht werden: Die Bewegung auf der Kreisbahn erfolgt mit konstanter Bahngeschwindigkeit. Die Bewegung
wird dann als gleichförmige Kreisbewegung bezeichnet. Die Begriffe noch einmal aufgelistet und mit ihren Einheiten versehen:
$$
\text{Kreisbogen} \; b \\
[b] = 1 \; \text{m} \\
\\
\text{Bahngeschwindigkeit} \; v \\
[v] = 1 \; \frac{\text{m}}{\text{s}} \\
\\
\text{Bahnbeschleunigung} \; a \\
[a] = 1 \; \frac{\text{m}}{\text{s}^2} \\
\\
\text{Radius} \; r \\
[r] = 1 \; \text{m} \\
\\
\text{Umlaufzeit} \; T \\
[T] = 1 \; \text{s} \\
\\
\text{Frequenz} \; f \\
[f] = 1 \; \text{Hz} \\
\\
\text{Winkelgeschwindigkeit} \; \omega \\
[\omega] = 1 \; \text{s}^{-1}
$$
Die Einheit der Frequenz lautet eigentlich $s^{-1}$, d.h. Anzahl von Umläufen pro Sekunde, wurde aber zu Ehren des Physikers
Heinrich Hertz nach diesem benannt: $1 Hz = 1 s^{-1}$.
Es gelten die folgenden Beziehungen:
\begin{align}
T = \frac{1}{f} \qquad &; \qquad f = \frac{1}{T} \\ \\
U &= 2 \pi r \\ \\
v = \frac{b}{t} = \frac{U}{T} &= \frac{2 \pi r}{T} = 2 \pi r f
\end{align}
Die neue Größe Winkelgeschwindigkeit bedarf einer näheren Beschreibung.
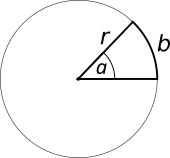Dem Winkel $\alpha$ wird das Verhältnis von Kreisbogen und Radius zugeordnet.
$$
\alpha \; \rightarrow \; \frac{b}{r}
$$
Mit der Winkelgeschwindigkeit wird ausgedrückt, welcher Winkel $\alpha$ in einer Zeit $t$ überstrichen wird, also $\omega = \frac{\alpha}{t}$. Mit
der Zuordnung $\alpha \rightarrow \frac{b}{r}$ wird das zu: $\omega = \frac{b}{r \cdot t}$. Da es sich um eine gleichförmige Geschwindigkeit
handelt, also in jeder Zeiteinheit der selbe Winkel überstrichen wird, folgt mit $b = 2 \pi r$, wenn $t = T$:
$$
\omega = \frac{2 \pi}{T}
$$
oder alternativ
$$
\omega = 2 \pi f
$$
Aus der letzten Gleichung folgt, dass die Frequenz und die Winkelgeschwindigkeit (auch als Kreisfrequenz bezeichnet) die gleiche Einheit
haben. Im Unterschied zur Frequenz bleibt es bei $\omega$ bei der Einheit $s^{-1}$.
Für die Beziehung zwischen Bahngeschwindigkeit und Winkelgeschwindigkeit folgt: \begin{align} v = 2 \pi r f \qquad &; \qquad \omega = 2 \pi f \\ v &= \omega \cdot r \end{align} Das Verhältnis Kreisbogen zu Radius ist ein anderer Ausdruck für den Winkel. Der Winkel wird in Grad (°) angegeben, $\frac{b}{r}$ ist eine einheitenlose Zahl und wird als Bogenmaß bezeichnet. Als Einheit dient der Radiant (rad). Aus dem Zusammenhang für den Vollkreis gilt: \begin{align} 360° &\hat{=} \; 2 \pi \; \text{ rad} \\ 180° &\hat{=} \; \pi \; \text{rad} \\ 90° &\hat{=} \; \frac{\pi}{2} \; \text{rad} \\ 30° &\hat{=} \; \frac{\pi}{6} \; \text{rad} \end{align}
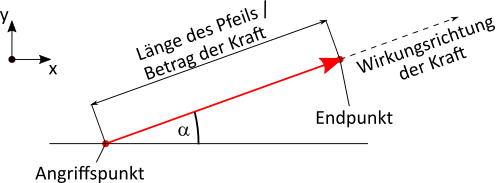Kräfte werden als Pfeile dargestellt. Die Länge des Pfeiles entspricht dabei dem Betrag der Kraft, die Richtung, in die
der Pfeil zeigt, entspricht der Wirkungsrichtung der Kraft.
Die Wirkungsrichtung wird immer bezüglich einer positiven x-Achse gemessen. Es ist also wichtig, sich bei der
Analyse der geometrischen Situation über ein Koordinatensystem klar zu werden. In den meisten Fällen wird die
x-Achse parallel zur Erdoberfläche bzw. parallel zu einer beliebigen Oberfläche und die y-Achse senkrecht dazu festgelegt.
In dem gezeigten Beispiel wirkt die Kraft unter einem Winkel von ca. 20°. Der Betrag der Kraft kann durch Messung der Pfeillänge ermittelt werden. Dabei muss dann der verwendete Maßstab beachtet werden.
Aufteilung in definierte Richtungen
Jede Kraft kann in alle möglichen Richtungen wirken. Wenn dann auch noch mehrere Kräfte auf einen Körper wirken, wird die Berechnung der Gesamtwirkung schnell kompliziert.
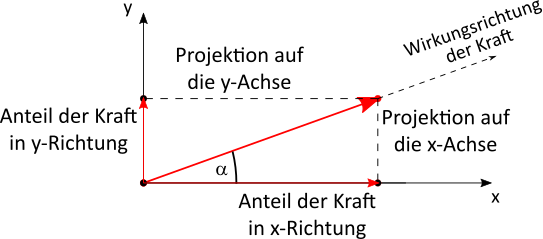
Daher wird jede beliebige Kraft zunächst in definierte Wirkungsrichtungen aufgeteilt. Diese definierten Richtungen sind die $x-$ und die $y-$Achse eines Koordinatensystems, bzw. die Richtung, in der eine Bewegung stattfinden kann und die Richtung senkrecht dazu. Wichtig ist daher, dass die definierten Wirkungslinien senkrecht zueinander sind.
Der Kraftpfeil wird auf die Koordinatenachsen projiziert. Dadurch entstehen zwei Kraftkomponenten: der Anteil der Kraft in $x-$ und in $y-$Richtung.
Berechnet werden die Anteile durch die folgenden Formeln: $$ F_x = F \cdot \cos \alpha \\ F_y = F \cdot \sin \alpha $$
Addition von Kräften
Die Addition von Kräften ist dann notwendig, wenn an einem Körper mehrere Kräfte angreifen und man die Aufgabe hat, die Gesamtwirkung, d.h die Gesamtkraft zu bestimmen. Die Gesamtkraft wird dann meist als resultierende Kraft $F_R$ bezeichnet.
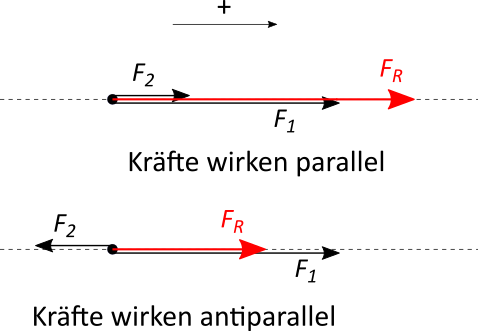
Wirken beide Kräfte auf einer Wirkungslinie, d.h. sie wirken parallel oder antiparallel, werden die Beträge der Kräfte einfach addiert. Es ist dabei zu beachten, dass auch hier eine positive Richtung angenommen wird. Wirkt die Kraft in diese positive Richtung, ist sie auch positiv (z.B. $F = 8 \text{ N}$). Wirkt sie dagegen in die entgegengesetzte Richtung, ist sie negativ (z.B. $F = -3 \text{ N}$).
Ist also $F_1 = 8 \text{ N}$ und $F_2 = 3 \text{ N}$, dann ist die resultierende Kraft $F_R = 8 + 3 = 11 \text{ N}$.
Ist dagegen $F_1 = 8 \text{ N}$ und $F_2 = -3 \text{ N}$, dann ist die resultierende Kraft $F_R = 8 + (-3) = 5 \text{ N}$.
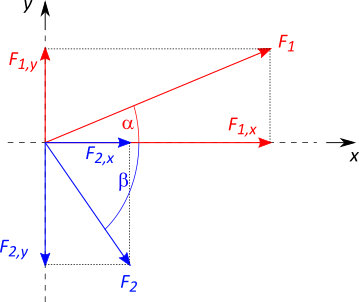
Bei beliebigen Wirkungsrichtungen wird jede Kraft zunächst in ihre $x-$ und $y-$Komponenten zerlegt. Die jeweilige $x-$Komponenten werden, da sie parallel oder antiparallel zueinander sind, einfach addiert, ebenso die jeweiligen $y-$Komponenten. Die dabei entstandenen Kraftkomponenten werden dann wieder zu einer resultierenden Kraft zusammengefasst.
Als Beispiel seien die beiden Kräfte $F_1$ und $F_2$ gegeben, die unter dem Winkel $\alpha$ bzw. $\beta$ wirken.
\begin{align} F_{1,x} &= F_1 \cdot \cos \alpha \\ F_{1,y} &= F_1 \cdot \sin \alpha \\ \\ F_{2,x} &= F_2 \cdot \cos \beta \\ F_{2,y} &= F_2 \cdot \sin \beta \\ \\ \\ F_{R,x} &= F_1 \cdot \cos \alpha + F_2 \cdot \cos \beta \\ F_{R,y} &= F_1 \cdot \sin \alpha + F_2 \cdot \sin \beta \end{align}Um die Komponenten der resultierenden Kraft wieder zusammenzufassen, wird der Satz des Pythagoras genutzt: $$ F_R = \sqrt{\left(F_{R,x} \right)^2 + \left( F_{R,y} \right)^2} $$ Für die Richtung der resultierenden Kraft gilt: $$ \tan \vartheta = \frac{F_{R,y}}{F_{R,x}} $$
Beispiel
Zwei Kräfte greifen an einem Körper an. Die erste Kraft wirkt mit dem Betrag $F_1 = 70 \text{ N}$ unter dem Winkel $\alpha = 20°$, die zweite Kraft mit $F_2 = 40 \text{ N}$ unter $\beta = -55°$.
Dann ist
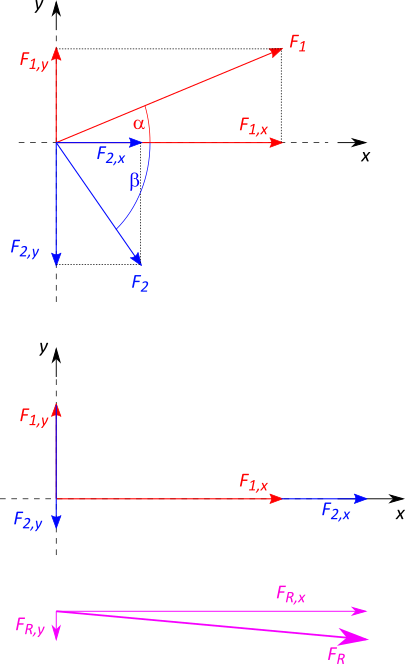\begin{align}
F_{1,x} &= 70 \text{ N} \cdot \cos 20° \\
F_{1,x} &= 65,78 \text{ N} \\
F_{1,y} &= 70 \text{ N} \cdot \sin 20° \\
F_{1,y} &= 23,94 \text{ N} \\ \\
F_{2,x} &= 40 \text{ N} \cdot \cos (-55°) \\
F_{2,x} &= 22,94 \text{ N} \\
F_{2,y} &= 40 \text{ N} \cdot \sin (-55°) \\
F_{2,y} &= -32,77 \text{ N} \\ \\ \\
F_{R,x} &= 65,78 \text{ N} + 22,94 \text{ N} \\
F_{R,x} &= 88,72 \text{ N} \\ \\
F_{R,y} &= 23,94 \text{ N} + \left( -32,77 \text{ N} \right) \\
F_{R,y} &= -8,83 \text{ N} \\ \\ \\
F_R &= \sqrt{\left(88,72 \text{ N} \right)^2 + \left( -8,83 \text{ N} \right)^2} \\
F_R &= 89,16 \text{ N} \\ \\
\vartheta &= \arctan \left( \frac{-8,83}{89,16} \right) \\
\vartheta &= -5,6°
\end{align}
Die resultierende Kraft wirkt mit einem Betrag von 89,16 N unter einem Winkel von -5,6°, also fast in x-Richtung.
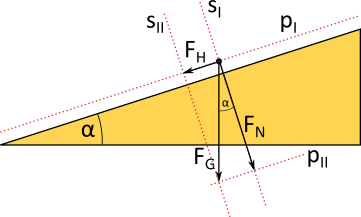Mit Hilfe der schiefen Ebene kann illustriert werden, wie und vor allem warum eine Kraft in zwei Teile aufgeteilt wird.
Für gerichtete Größen wie die Kraft, aber auch für die Geschwindigkeit oder die Beschleunigung, sind zwei Richtungen wesentlich: Erstens die Richtung, in der eine Bewegung oder eine Wirkung stattfindet bzw. stattfinden soll und zweitens die Richtung senkrecht dazu.
Bei der schiefen Ebene ist das erstens die Richtung parallel zur Ebene (die Richtung, in der eine Bewegung abläuft) und die Richtung senkrecht dazu. In der Skizze ist der Massepunkt, der den Körper symbolisiert, der Ausgangspunkt für zunächst einmal die Gewichtskraft $F_G$. Die Länge des Kraftpfeils entspricht dem Betrag der Gewichtskraft. Sie ist die einzig wirkende Kraft in dieser Situation. Die Richtung parallel zur Ebene wird durch die rot punktierte Linie $p_I$ dargestellt, die Richtung senkrecht dazu durch die Linie $s_I$. Beide Linien verlaufen durch den Massepunkt.
Durch den Endpunkt des Gewichtskraftpfeils wird nun noch eine Linie $p_{II}$ parallel zur Ebene gezeichnet, genauso wie eine Linie $s_{II}$ senkrecht dazu. Insgesamt entsteht so ein rot punktiertes Rechteck mit dem Gewichtskraftpfeil als eine der Diagonalen.
Der Winkel $\alpha$ bezeichnet den Neigungswinkel, den die Ebene bezüglich der waagerechten Unterlage (der Erdoberfläche) aufweist. Der Winkel taucht in dem rot punktierten Rechteck wieder auf zwischen dem Gewichtskraftpfeil und den Linien $s_I$ (oben rechts) bzw. $s_{II}$ (unten links).
Die beiden in das Rechteck eingezeichneten Kräfte $F_H$ und $F_N$ sind nun die beiden Kräfte, die in die Bewegungs- oder Wirkungsrichtung $\left( F_H \right)$ bzw. senkrecht auf die Ebene $\left( F_N \right)$ zeigen. Berechnet werden sie durch die folgenden Gleichungen: $$ F_H = F_G \cdot \sin \alpha \\ \\ F_N = F_G \cdot \cos \alpha $$
Die Kraft $F_H$ wird Hangabtriebskraft genannt, also ist es die Kraft, die dafür sorgt, dass die Bewegung entlang der Ebene nach unten verläuft. Für die Kraft $F_N$ wird die Bezeichnung Normalkraft genutzt. (Mathematisch ist die Normale allerdings eine Richtung, die senkrecht von einer Ebene wegzeigt. Die Normalkraft zeigt hingegen auf die Ebene, ist also genau entgegengesetzt. Unbeachtet der Tatsache hat sich aber die Bezeichnung in der Physik eingebürgert. Wichtig ist damit die Wirkungsrichtung, die senkrecht zu einer Oberfläche ist.) Die Normalkraft sorgt dafür, dass der Körper auf die Oberfläche gedrückt wird. Es ist also so etwas wie eine Andruckkraft.
Die Wirkung von $F_H$ ist dann z.B. eine Beschleunigung einer Bewegung, was im nächsten Abschnitt thematisiert wird. $F_N$ wirkt indirekt als Reibkraft, die eine Bewegung behindert bzw. verhindert. Das wird im Abschnitt über die Reibung erläutert.
Eine Bewegung ist gekennzeichnet durch die Geschwindigkeit $v = \frac{\Delta s}{\Delta t}$. Ist der in einer Zeitspanne $\Delta t$ zurückgelegte Weg $\Delta s$ konstant, spricht man von einer gleichförmigen Bewegung. Soll sich die Bewegung und damit die Geschwindigkeit ändern, muss eine Beschleunigung $a = \frac{\Delta v}{\Delta t}$ vorhanden sein. Mit dem zweiten Newtonschen Axiom $F=m \cdot a$ führt das zu einer Kraft, die damit für die Bewegungsänderung des betrachteten Körpers sorgt.
Beispiel 1
Ein Auto mit der Masse $m = 1200 \text{ kg}$ beschleunigt von 0 auf 100 km/h in $t = 8 \text{ s}$. Bestimmt werden soll die Beschleunigungskraft des Motors.
Ansatz:
Am Ende soll die Kraft berechnet werden, also $F = m \cdot a$. Die Masse ist bekannt, die Beschleunigung nicht. Aber es gilt:
$a = \frac{\Delta v}{\Delta t}$.
Da $\Delta t$ bekannt ist (8 s), muss nur noch $\Delta v$ bestimmt werden: \begin{align} \Delta v &= 100 - 0 \; \frac{\text{km}}{\text{h}} \\ \Delta v &= \frac{100}{3,6} \; \frac{\text{m}}{\text{s}} \\ \Delta v &= 27,78 \; \frac{\text{m}}{\text{s}} \end{align} Es folgt insgesamt: \begin{align} F &= m \cdot a \\ F &= m \cdot \frac{\Delta v}{\Delta t} \\ F &= 1200 \; \text{kg} \cdot \frac{28,78 \; \frac{\text{m}}{\text{s}}}{8 \; \text{s}} \\ F &= 4167 \; \text{N} \\ \\ F &\approx 4,17 \; \text{kN} \end{align} Das Auto wird also mit ungefähr 4,17 kN angetrieben.
Beispiel 2
Das Auto soll nun abgebremst werden. Zum Bremsen steht eine Kraft von $F = 10000 \; \text{N}$ zur Verfügung. Die Frage ist, welchen Weg das Auto noch zurücklegt, wenn es sich mit $v = 50 \; \frac{\text{km}}{\text{h}}$ bewegt.
Ansatz:
Es gilt $F = m \cdot a$. Für die beschleunigte Bewegung gelten die beiden Zusammmenhänge: (I) $s = \frac12 a \cdot t^2$ und (II) $v = a \cdot t$.
Fasst man die beiden Gleichungen zusammen, erhält man
\begin{align}
s &= \frac12 a \cdot t^2 &\qquad \qquad v &= a \cdot t \\ \\
s &= \frac12 a \cdot t^2 &\qquad \qquad t &= \frac{v}{a} \\ \\
s &= \frac12 a \cdot \frac{v^2}{a^2} \\ \\
s &= \frac{v^2}{2a}
\end{align}
Mit $a = \frac{F}{m}$ führt das zu der Berechnung:
\begin{align}
s &= \frac{v^2 \cdot m}{2F} \\ \\
s &= \frac{\left( \frac{50}{3,6} \; \frac{\text{m}}{\text{s}} \right)^2 \cdot 1200 \; \text{kg}}{2 \cdot 10000 \; \text{N}} \\ \\
s &= 11,574 \; \text{m}
\end{align}
Es fährt also noch gut 11,6 m bis zum Stillstand.
Die Reibungskraft sorgt immer und in jedem Fall dafür, dass Bewegungen abgebremst werden.
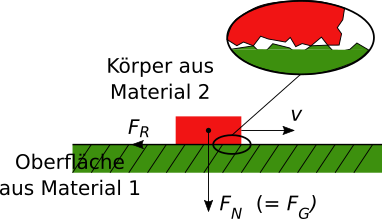
In der Abbildung wird die Bewegung mit der Geschwindigkeit $v$ durch die Reibkraft $F_R$ abgebremst.
Die Reibungskraft entsteht durch die mikroskopische Gestalt der beiden Kontaktflächen, die sich ineinander verhaken, wenn sich die Oberflächen
gegeneinander bewegen. Die Kraft, die den Körper auf die Oberfläche drückt, wird Normalkraft $F_N$ genannt, in Anlehnung an den mathematischen
Begriff der Normalen, der Richtung senkrecht zu Oberflächen. Die Form der Kontaktflächen, die Materialien von Körper und Oberfläche sowie
der Zustand der Kontaktflächen (nass, trocken, geschmiert, ...) definieren, wie die Normalkraft als Reibungskraft wirkt.
Aus der Gewichtskraft, die immer in Richtung Erdmittelpunkt wirkt, wird die Normalkraft bestimmt:
$$
F_N = F_G \cdot \cos \alpha
$$
Aus der Normalkraft wird die Reibungskraft bestimmt:
$$
F_R = \mu \cdot F_N
$$
Insgesamt erhält man somit:
$$
F_R = m \cdot g \cdot \mu \cdot \cos \alpha
$$
mit $\mu$ als dem sogenannten Reibkoeffizienten, der die Materialpaarung und die Kontakteigenschaften berücksichtigt. Der Winkel $\alpha$ ist
der Neigungswinkel der Oberfläche zur Waagerechten (dazu: Schiefe Ebene).
Die Reibungskraft wirkt als Bremskraft analog zu der Beschleunigungskraft.
Für eine etwas detailliertere Betrachtung der Reibung müssen drei unterschiedliche Szenarien betrachtet werden:
Beispiel
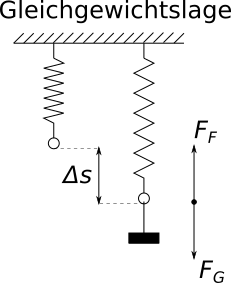Wird ein Körper mit einer Masse $m$ an eine Feder gehängt, verlängert sich die Feder um einen bestimmten Weg $s$. Die Verlängerung ist
proportional zur angehängten Masse und wegen $F_G = m \cdot g$ auch proportional zur Gewichtskraft.
Wenn der Körper an die Feder gehängt wird, befindet er sich nach einer Weile in Ruhe. Dann wirkt insgesamt keine resultierende Kraft auf ihm.
Die Gewichtskraft wird durch die Kraft, die die Feder ausübt ($F_F$), ausgeglichen: $F_G = - F_F$. Das System befindet sich im Gleichgewicht und
es gilt $s \sim - F_F$.
Die Federkraft ist die Kraft, mit der die Feder versucht, ihre aufgezwungene Verlängerung rückgängig zu machen. Da die
Feder aber natürlich nicht agieren kann, sondern nur auf die Belastung durch die Masse des angehängten Körpers reagiert, führt das dazu, dass die
Federkraft so groß ist, dass sie die Gewichtskraft gerade ausgleicht. Die Feder wird also nicht weiter verlängert und befindet sich in einer
Gleichgewichtslage.
Für die Ermittlung des Proportionaltätsfaktors wird eine beispielhafte Feder mit unterschiedlichen Massen belastet und die jeweilige Verlängerung notiert. Es entsteht z.B. die folgende Tabelle:
| Masse in kg |
Federkraft in N |
Verlängerung in m |
|---|---|---|
|
0,05 0,10 0,15 0,20 0,25 |
0,4905 0,9810 1,4715 1,9620 2,4525 |
0,090 0,182 0,270 0,363 0,451 |
Wichtig ist vor allem die Feststellung, dass die Feder eine Kraft ausübt, die sich der Verlängerung bzw. der Verkürzung der Feder entgegenstellt. Daher kommt das Minuszeichen. Die Größe der Kraft ist dabei nicht konstant, sondern hängt von der Größe der Verlängerung / Verkürzung ab.
Dieser Zusammenhang gilt nicht nur für Federn an sich, sondern für alle federnden bzw. elastischen Systeme. In bestimmten Bereichen ist z.B. auch ein Stahlstab elastisch: ein Stahlstab mit einem Querschnitt von einem Quadratmillimeter kann sich bei einer Belastung von ca. 1000 N um etwa 2 % elastisch verlängern. Die Werte hängen natürlich von der Stahlsorte und von der Herstellung / Behandlung des Stahls ab und sind lediglich beispielhaft zu verstehen.
Beispiel
Eine Feder wird durch eine Masse von 5 kg belastet und verlängert sich dabei um 5 cm. Bestimmt werden soll die Federkonstante.
Ansatz:
Es gilt $F = D \cdot s$. Umgeformt: $D = \frac Fs$
\begin{align}
D &= \frac{m \cdot g}{s} \\ \\
D&= \frac{5 \; \text{kg} \cdot 9,81 \; \frac{\text{m}}{\text{s}^2}}{0,05 \; \text{m}} \\ \\
D&= 981 \; \frac{\text{N}}{\text{m}}
\end{align}
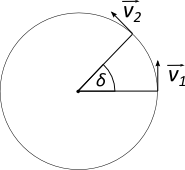Bei der Bewegung im Kreis muss man unterscheiden zwischen der Bewegung entlang der kreisförmigen Bahn und der Bewegung, die das Objekt immer
wieder auf die Kreisbahn zwingt.
Zur Klärung: Jede Bewegung, auf die keine Kräfte wirkt, ist konstant. Das heißt, dass es keine Geschwindigkeitveränderung
und auch keine Richtungsveränderung gibt. Jedes Objekt ohne Krafteinwirkung wird sich also mit konstanter Geschwindigkeit in einer geraden Linie
weiter bewegen. Beschreibt das Objekt aber eine Kreisbahn, gibt es eine Richtungsänderung, also muss auch eine Beschleunigung existieren, die diese
Richtungsänderung bewirkt.
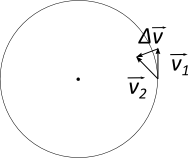
Das $\Delta v$ bezeichnet hier die benötigte Geschwindigkeitsänderung, damit das Objekt auf der Kreisbahn bleibt.
Trägt man nicht die Geschwindigkeiten auf sondern den zurückgelegten Weg, erhält man die untenstehende Abbildung. Dort wird der Weg, den das Objekt an dem Punkt $P_1$ im Zeitintervall $\Delta t$ zurücklegen würde, mit $s_1$ bezeichnet. Es ist zu beachten, dass die Bewegung entlang der Kreisbahn gleichförmig ist.
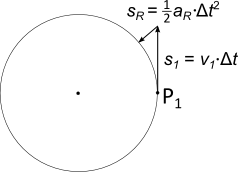$s_R$ ist die Bezeichnung für den dann notwendigen Weg
zurück auf die Kreisbahn. Die Richtung von $s_R$ ist senkrecht zur Kreisbahn bzw. genau auf den Kreismittelpunkt. Da es sich hier um eine
Richtungsänderung der Bewegung handelt, ist diese Bewegung eine gleichmäßig beschleunigte Bewegung.
Werden die beiden eingezeichneten Wege jeweils ergänzt durch den Radius des Kreises ergibt sich ein rechtwinkliges Dreieck. Für dieses muss der Satz
des Pythagoras gelten, also:
$$
r^2 + \left( v_1 \cdot \Delta t \right)^2 = \left( r + \frac{1}{2} a_R \cdot \Delta t^2 \right)^2
$$
Rechts von Gleichheitszeichen steht eine binomische Formel. Multipliziert man diese aus, erhält man den folgenden Ausdruck:
$$
r^2 + v_1^2 \cdot \Delta t^2 = r^2 + 2 \cdot r \cdot \frac{1}{2} a_R \cdot \Delta t^2 + \frac{1}{4} a_R^2 \cdot \Delta t^4
$$
Der Term $r^2$ steht auf beiden Seiten der Gleichung und kürzt sich heraus. Desweiteren gibt es in jedem Summanden den Term $\Delta t^2$, der ebenfalls
herausgekürzt wird. Es entsteht die Gleichung:
$$
v_1^2 = 2 \cdot r \cdot \frac{1}{2} a_R + \frac{1}{4} a_R^2 \cdot \Delta t^2
$$
Da eine Bewegung auf einer Kreisbahn nicht in einem Sägezahnmuster abläuft, sondern
eine kontinuierliche Bewegung ist, wird der Term $\Delta t = 0$ gesetzt.
Somit erhält man: \begin{align} v_1^2 & = 2 \cdot r \cdot \frac{1}{2} a_R \\ v_1^2 & = r \cdot a_R \\ a_R & = \frac{v_1^2}{r} \end{align} Da die Bedingung für $a_R$ natürlich zu jedem Zeitpunkt und für jeden Punkt auf der Kreisbahn gilt, folgt: $$ a_R = \frac{v^2}{r} \quad \text{oder} \quad a_Z = \frac{v^2}{r} $$ Diese Größe nennt man Radialbeschleunigung oder Zentripetalbeschleunigung und ist notwendig, wenn es eine Kreisbewegung geben soll. Die Einheit ist wie bei der (Bahn-)Beschleunigung Meter pro Sekunde zum Quadrat. $$ \text{Radialbeschleunigung} \; a_R \\ \text{Zentripetalbeschleunigung} \; a_Z \\ [a_Z] = 1 \; \frac{ \text{m}}{ \text{s}^2} $$
Nach dem zweiten Newtonschen Axiom gilt: $$ F = m \cdot a $$ Mit der Zentripetalbeschleunigung $a_Z$ gibt es also eine Zentripetalkraft $F_Z$ (bzw. eine Zentralkraft oder Radialkraft), für die gilt: $$ F_Z = m \cdot a_Z $$ Also: $$ \text{Zentripetalkraft} \; F_Z \\ [F_Z] = 1 \; \text{N} $$ Wie schon bei der Zentripetalbeschleunigung ist die Zentripetalkraft notwendig, damit eine Kreisbewegung stattfinden kann.
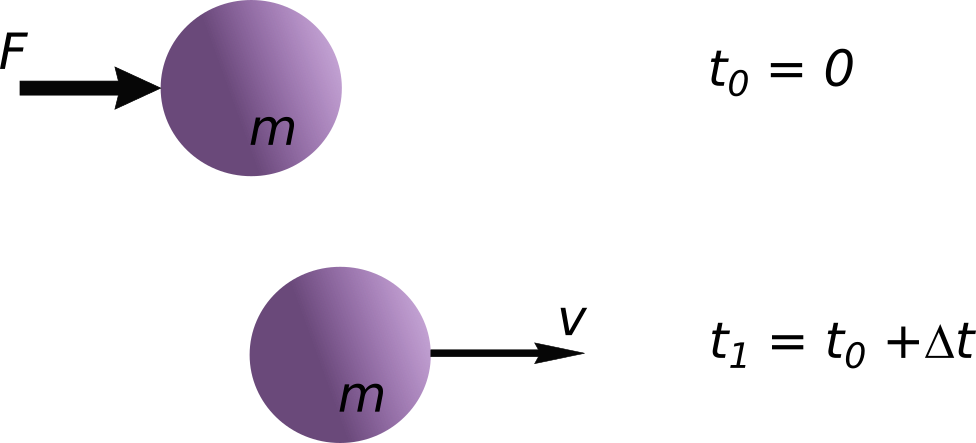
Der Bewegungszustand wird im Allgemeinen durch die Geschwindigkeit $v$ beschrieben. Mit den sogenannten Bewegungsgleichungen $s = \frac12 a t^2$ und $v = at$ können Bewegungen analysiert und berechnet werden. Die Masse $m$ des Körpers, der sich im Bewegung befindet, wird dabei nicht betrachtet.
Die Wirkung des sich bewegenden Körpers hängt aber nicht nur von seiner Geschwindigkeit ab, sondern ebenso von seiner Masse. Der Impuls $p$ beschreibt den Bewegungszustand des Körpers mit der Masse $m$; es gilt: $$ p = m \cdot v $$ Die Geschwindigkeit $v$ ist eine gerichtete, vektorielle Größe. Mit der skalaren Größe Masse folgt, dass der Impuls eine vektorielle Größe ist. Damit gilt: $$ \vec p = m \cdot \vec v $$ Der Impuls eines Körpers wirkt in dieselbe Richtung wie seine Bewegung.
Der Impuls kann von einem Körper auf einen anderen Körper ganz oder teilweise übertragen werden. Die Übertragung geschieht durch den Kraftstoß.
Der Kraftstoß ist das Produkt aus der wirkenden (konstanten) Kraft und der Dauer der Kraftwirkung. Es gilt:
$$
\vec F \cdot \Delta t = m \cdot \vec v
$$
Der Kraftstoß bewirkt eigentlich eine Bewegungsveränderung. Die Veränderung erfolgt in die Richtung, in die die Kraft wirkt. Für den Kraftstoß
gilt also
$$
\vec F \cdot \Delta t = m \cdot \Delta \vec v
$$
Der Kraftstoß kann auch angewendet werden, wenn z.B. ein Körper von außen gestoßen wird und dadurch eine Änderung seiner Bewegung erfährt. Dies kann entweder eine Änderung des Geschwindigkeitsbetrags sein oder auch der Bewegungsrichtung.
Der Impuls ist eine Erhaltungsgröße, genau wie die Energie oder die Masse. Für die Übertragung des Impulses von einem Körper auf einen anderen gibt es zwei Grenzfälle:
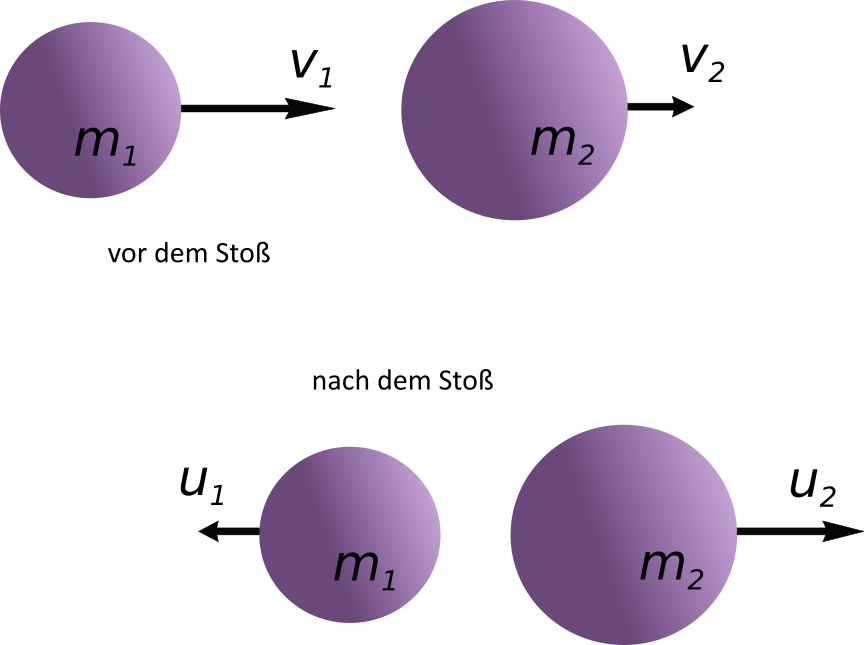\begin{align}
p_v &= p_n \\
m_1 \cdot v_1 + m_2 \cdot v_2 &= m_1 \cdot u_1 + m_2 \cdot u_2 \\
\end{align}
Dabei sind $m_1$ und $m_2$ die Massen der beiden am Stoß beteiligten Körper, $v_1$ und $v_2$ die Geschwindigkeiten der Körper vor
dem Stoß sowie $u_1$ und $u_2$ die Geschwindigkeiten der Körper nach dem Stoß.
Die (meistens) einzigen unbekannten Größen sind die Geschwindigkeiten nach dem Stoß: $u_1$ und $u_2$
Der Impulserhaltungssatz kann umgestellt und sortiert werden: $$ m_1 \left( v_1 - u_1 \right) = - m_2 \left( v_2 - u_2 \right) $$ Man hat also eine Gleichung mit zwei Unbekannten, die somit nicht zu lösen ist. Um dennoch eine Lösung zu erhalten betrachtet man die beiden Grenzfälle.
Für diesen Stoß gilt, dass die gesamte kinetische Energie beider Körper bei dem Stoß erhalten bleibt. Das führt zu der Gleichung: $$ \frac12 \cdot m_1 \cdot v_1^2 + \frac12 \cdot m_2 \cdot v_2^2 = \frac12 \cdot m_1 \cdot u_1^2 + \frac12 \cdot m_2 \cdot u_2^2 $$ Der Energieerhaltungssatz kann auch umgestellt werden: \begin{align} \frac12 \cdot m_1 \cdot v_1^2 - \frac12 \cdot m_1 \cdot u_1^2 &= \frac12 \cdot m_2 \cdot u_2^2 - \frac12 \cdot m_2 \cdot v_2^2 \\ \frac12 \cdot m_1 \left( v_1^2 - u_1^2 \right) &= \frac12 \cdot m_2 \left( u_2^2 - v_2^2 \right) \\ \frac12 \cdot m_1 \left( v_1^2 - u_1^2 \right) &= - \frac12 \cdot m_2 \left( v_2^2 - u_2^2 \right) \\ m_1 \left( v_1^2 - u_1^2 \right) &= - m_2 \left( v_2^2 - u_2^2 \right) \end{align} Wendet man nun die dritte binomische Formel an, folgt: $$ m_1 \left(v_1 - u_1 \right) \left(v_1 + u_1 \right) = - m_2 \left( v_2 - u_2 \right) \left( v_2 + u_2 \right) $$
Aus dem Impulserhaltungssatz folgt also:
$$
m_1 \left( v_1 - u_1 \right) = - m_2 \left( v_2 - u_2 \right)
$$
und aus dem Energieerhaltungssatz:
$$
m_1 \left(v_1 - u_1 \right) \left(v_1 + u_1 \right) = - m_2 \left( v_2 - u_2 \right) \left( v_2 + u_2 \right)
$$
Wenn man die erste Gleichung in die zweite Gleichung einsetzt und umformt, entsteht
$$
\left(v_1 + u_1 \right) = \left( v_2 + u_2 \right)
$$
Nach $u_2$ umgestellt:
$$
u_2 = v_1 + u_1 - v_2
$$
und in dem Impulserhaltungssatz eingesetzt:
\begin{align}
m_1 \left( v_1 - u_1 \right) &= - m_2 \left( v_2 - u_2 \right) \\ \\
m_1 \left( v_1 - u_1 \right) &= - m_2 \left( v_2 - \left( v_1 + u_1 - v_2 \right) \right) \\ \\
m_1 \cdot v_1 - m_1 \cdot u_1 &= - m_2 \cdot v_2 + m_2 \cdot v_1 + m_2 \cdot u_1 - m_2 \cdot v_2 \\ \\
m_1 \cdot v_1 + m_2 \cdot v_2 + m_2 \cdot v_2 - m_2 \cdot v_1 &= m_2 \cdot u_1 + m_1 \cdot u_1 \\ \\
\left( m_1 - m_2 \right) v_1 + 2 m_2 v_2 &= \left( m_1 + m_2 \right) u_1
\end{align}
$$
\text{➜ }\qquad u_1 = \frac{\left( m_1 - m_2 \right) v_1 + 2 m_2 v_2}{\left( m_1 + m_2 \right)}
$$
Analog ergibt sich in einer entsprechenden Umformung:
$$
\text{➜ }\qquad u_2 = \frac{\left( m_2 - m_1 \right) v_2 + 2 m_1 v_1}{\left( m_1 + m_2 \right)}
$$
Und:
$$
\text{➜ }\qquad v_1 + u_1 = v_2 + u_2
$$
In diesem Fall gilt der Energieerhaltungssatz nicht mehr, da kinetische Energie „verloren“ geht. Allerdings beschreibt der Grenzfall den Stoß so, dass sich beide Körper nach dem Stoß als ein Körper weiterbewegen. Nach dem Stoß gibt es also nur eine Geschwindigkeit $u$. Der Impulserhaltungssatz sieht dann so aus: $$ m_1 \cdot v_1 + m_2 \cdot v_2 = \left( m_1 + m_2 \right) u $$ Für die Geschwindigkeit nach dem Stoß folgt: $$ \text{➜ }\qquad u = \frac{m_1 \cdot v_1 + m_2 \cdot v_2}{\left( m_1 + m_2 \right)} $$
Eine Kugel der Masse $m_1 = 200 \text{ g}$ trifft mit $v_1 = 3 \; \frac{\text{m}}{\text{s}}$ elastisch und zentral auf eine ruhende Kugel der Masse $m_2 = 500 \text{ g}$. Also ist $v_2 = 0$. Berechnen Sie die Geschwindigkeiten der Kugeln nach dem Stoß.
Es gilt: $$ u_1 = \frac{\left( m_1 - m_2 \right) v_1 + 2 m_2 v_2}{\left( m_1 + m_2 \right)} $$ Mit den bekannten Werten: \begin{align} u_1 &= \frac{\left( 0,2 \text{ kg} - 0,5 \text{ kg} \right) \cdot 3 \; \frac{\text{m}}{\text{s}} + 2 \cdot 0,5 \text{ kg} \cdot 0}{\left( 0,7 \text{ kg} \right)} \\ \\ u_1 &= - 1,29 \; \frac{\text{m}}{\text{s}} \end{align} Die Geschwindigkeit der zweiten Kugel: \begin{align} u_2 &= \frac{\left( m_2 - m_1 \right) v_2 + 2 m_1 v_1}{\left( m_1 + m_2 \right)} \\ \\ u_2 &= \frac{\left( 0,5 \text{ kg} - 0,2 \text{ kg} \right) \cdot 0 + 2 \cdot 0,2 \text{ kg} \cdot 3 \; \frac{\text{m}}{\text{s}}}{\left( 0,7 \text{ kg} \right)} \\ \\ u_2 &= 1,71 \; \frac{\text{m}}{\text{s}} \end{align} Kugel 1 bewegt sich also mit $u_1 = - 1,29 \; \frac{\text{m}}{\text{s}}$, d.h. sie prallt zurück, während sich Kugel 2 mit $u_2 = 1,71 \; \frac{\text{m}}{\text{s}}$ in die ursprüngliche Richtung bewegt.
Ein Güterwaggon rollt mit $v_1 = 0,2 \; \frac{\text{m}}{\text{s}}$ auf einen zweiten ruhenden Waggon und koppelt an. Die Massen sind: $m_1 = 12500 \text{ kg}$ und $m_2 = 19000 \text{ kg}$. Mit welcher Geschwindigkeit rollen beide gemeinsam weiter?
Mit der Formel für den inelastischen Stoß folgt: \begin{align} u &= \frac{m_1 \cdot v_1 + m_2 \cdot v_2}{\left( m_1 + m_2 \right)} \\ \\ u &= \frac{12500 \text{ kg} \cdot 0,2 \; \frac{\text{m}}{\text{s}} + 19000 \text{ kg} \cdot 0}{\left( 31500 \text{ kg} \right)} \\ \\ u &= 0,08 \; \frac{\text{m}}{\text{s}} \end{align} Bestimmt man für diesen Fall die kinetischen Energien vorher $\left( E_{kin} = 250 \text{ J} \right)$ und nachher $\left( E_{kin} = 100,8 \text{ J} \right)$, stellt man fest, dass ca. 60 % der kinetischen Energie $\left( \frac{250 \text{ J} - 100,8 \text{ J}}{250 \text{ J}} = 0,5968 \right)$ im Kopplungsprozess „verloren“ gegangen ist.
➜ hier
© mondbrand MMXIX